2019入試分析算数

目次

開成中
麻布中
武蔵中
桜䕃中
女子学院
雙葉中
筑波大付属駒場中
駒場東邦中
渋谷教育学園渋谷中
豊島岡女子学園中
早稲田中
早稲田実業中
慶應義塾中等部
渋谷教育学園幕張中
聖光学院中
栄光学園中
浅野中

算数　総評

　今年の首都圏算数入試問題の傾向を一言で言うと、例年よりも易しくなった学校が多いといえます。これまでほとんど見られなかったような基本問題が出されたり、塾などで指導の際に「捨て問」として扱われるだろうレベルの問題の割合がかなり減ったりしています。
　算数の問題が難しくなりがちなのは「思考力」を問う問題を出そうとするためです。しかし入試は選抜試験であるという観点からすると、難しすぎる問題は一部の受験生を除き手が付けられず、合否ライン近辺での弁別性が低くなってしまい、結果として算数ができない受験生が合格、入学してしまう可能性が高くなります。実際に過去のデータを見ると、少し易しいと感じる程度の方が合格者平均と受験者平均の差が大きくなっており、かつ平均点が上がることで算数が極端にできない受験生が他科目だけで合格する可能性が減ります。この点からすると易化傾向は合理的な判断ともいえます。
　また、問題の難化がもたらした弊害についても考慮する必要があります。難関校で出された問題は最初の時点では思考力を問う問題になります。しかしそれが塾等のテキストに掲載されることで身につける手法と同一視されるようになってしまいます。するとそれより難しい問題で思考力を問おうとしますが、また塾のテキストに掲載される、といういたちごっこになってしまいます。結果として塾のテキストは年々分厚くなり、１問１問をじっくりと考える余裕がなくなった結果、よくわからないままの暗記に陥りやすいのが現状です。

　今年の問題に目を転じると、易しかった学校が多いといっても、一部を除けば塾の確認テストのような覚えた手法を機械的に当てはめれば解けるような問題ばかりが出たわけではありません。問題の状況をきちんと読み取り、それに基づいて図をかく、整理する、類似の設定を想起して適用してみるという、算数の問題を考える上で本来当たり前のことを当たり前にできれば解きやすくなっていたということです。高度な思考力までは求めずに「捨て問」にされないレベルに設定したことで、正当な学習や思考する姿勢が評価されやすい問題になったということができます。
　一方で、従来通りに思考力を試そうとした学校も見られますが、これらの学校では「読解力」が重要なキーワードになりつつあります。例えば開成や桜蔭などでは問題が長文化し、状況把握や整理が高いレベルで試されました。また麻布や栄光学園などは最終問題単独では難しくても、設問で丁寧に誘導することで、出題者の意図をくみ取りながら考えられれば解けるよう工夫がなされていました。単に知識を吐き出すのではなく、適切な状況分析の下で持っている知識を活用して考えさせる方向性は大学入試改革に近いといえます。
　また、問題が易しくなると算数に特に強い受験生を取りこぼす可能性が出てきてしまいます。今年は巣鴨や世田谷学園などでも算数１科目入試が導入されましたが、一般の４科目入試では合否ラインでの弁別性を上げつつ、算数が特によくできる「尖った」受験生も拾おうとする試みといえます。また近年穏やかな出題が続いていた筑駒や女子学院では再び難化しており、今年の全体的な易化傾向はどういう問題を出せば思考力（の芽）がある受験生がとれるか試行錯誤している段階で起こったことと考えられます。

　この易化傾向が来年も続くのか、それとも揺り戻しが起こるのかはわかりません。しかし、いずれにせよ問題と解法の１対１対応の暗記ではなく、どんなレベルであれきちんと思考することができる受験生を求めていることは確かです。
　そのためにはまずは１つ１つの解法について、どういう場合に使えるものか、なぜその方法で解くことができるのかといった点をきちんと理解しながら進めることが必要になります。塾の確認テストだけであれば数字替えに近い問題が多いため暗記で乗り切ることも可能ですが、それでは活用できる解法にはならないことを肝に銘じる必要があります。また一方的に解き方を教わるだけでは思考力にはつながりません。自ら手を動かす作業を通じながらじっくりと考える時間をとることも大切です。
　このように１問１問にじっくりと時間をかけて学習することは多量のカリキュラムをこなす必要のある状況では難しいことであり、塾のテストで点をとるだけなら回り道にも見えます。しかしこれらのスローな学習の土台は過去問演習を中心とした初見問題に取り組む段階で真価を発揮します。スピーディーな処理力もある程度必要ですが、その前段階での確実な理解と、時には手を動かしながらじっくり考える時間、心の余裕を持つようにしてください。

開成中

　開成中は毎年のように出題傾向が大きく変わります。昨年は典型問題ばかりの易しい問題でしたが、今年は一転して読解力・処理力・論理的思考すべてがバランスよく問われる重厚なセットとなりました。易しかった昨年と比べれば85点満点で受験者平均51.0（昨年62.0）、合格者平均64.6（同73.9）と難化しましたが、過去数年で見れば平均的な得点率といえます。
　今年から問題が「問題用紙2枚」から「問題冊子」へと変更になりましたが、スペースに余裕ができたためか全体に問題文が長くなりました。問題の状況把握、出題者の誘導をくみ取ることが強く求められており、2020年度より施行される「大学入学共通テスト」に似た雰囲気だったといえます。

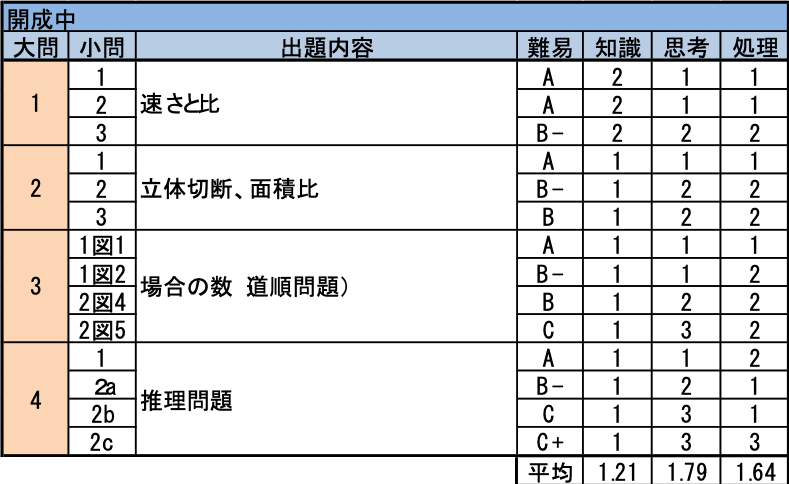
1. 兄弟でスイカを運ぶというユニークな設定になっていますが、比を用いて速さを扱うことに慣れていれば素直に解ける問題であり、落とせません。
2. 立体切断自体は定番のテーマですが、投影図の面積から元の直方体の辺の長さを特定させるという異なった切り口からの出題になっています。
3. 素直な道順問題である(1)は落とせませんが、(2)では途中で1回戻るというひねりが加わっています。どこで戻るかで場合分けしても解けますが、(1)の立体の場合との関連性に注目できると鮮やかに解くことができます。
4. ゲームに関する推理問題です。実は(1)が単なる作業ではなく(2b)のヒントとなっていることに気づくと糸口が見えますが、背理法など数学的に高度な論理力が要求される難しい問題です。

　最初に述べた通り開成中の問題は毎年のように出題傾向が変わるので、今年の問題だけを見て対策を考えることは危険です。とはいえ昨年のように定番問題が並ぶ場合があること、および今年の１、２のように定番問題をベースに考えさせる問題も出されることから、塾で出てくるタイプの問題については発展的な問題も含めて確実にできるよう仕上げることが必要です。定型的な手法については6年夏までに身につけ、その後は過去問等で煩雑な処理を要する場合であっても、丁寧な調べつくしが求められる場合であっても確実に処理しきれるようにしていきましょう。定番問題が出た場合の開成受験生の得点率は非常に高いです。
　一方で6年夏以降に本格的に過去問に取り組む段階になると、今年の４や一昨年の２のようなこれまで全く見たことがないタイプの問題に面食らうかもしれません。これらの問題について入試の前に同じような問題を解いたことがある人はまずいないので、その場での対応力もつけていく必要があります。
　問題を解く際に問題文を丁寧に読むことは当然ですが、特にこのような問題では３(1)、４(1)のように出題者がヒントを散りばめていることも多いです。従って、似た状況がどこかになかったか、この1文は何のために書いているのかなど、あらゆる方向にアンテナを張り巡らしながら考える練習を積んでおく必要があります。
　このような問題は汎用性がないため、開成の過去問を除くと一部の学校でたまに出される程度です。わからなかったときに解説を見て解き方を理解し覚える学習には何の意味もない問題でもあるので、1問1問に対して簡単にあきらめず粘り強く考えてみるようにしてください。

麻布中

　例年、思考力、試行錯誤力が問われる問題が出題され、単元では、数の性質、規則性、平面図形、立体図形、速さの問題がよく出題されます。ほとんどが、式や考え方を記述するため、部分点を意識して答案を作ることも重要です。今年も例年通りの出題でしたが、大問が1問減り5問になったことで、より時間をかけて丁寧に解答することができたかがポイントとなります。

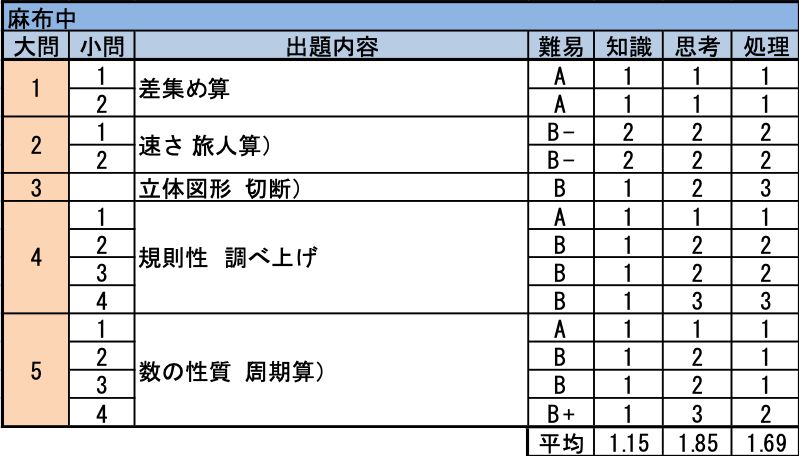
1. 短時間で解きたい必答問題です。
2. ダイヤグラムを利用し、相似比を使って解けば特に難しい問題ではありません。こちらも麻布受験者であれば必答問題です。
3. 立体図形の出題は珍しくありませんが、立体図形の切断の出題は珍しいため、意外と時間がかかった受験生もいるのではないでしょうか。
4. 誘導に沿って解き進める麻布らしい問題です。導かれるままに解けば最後まで解ける、麻布の先生の優しさに溢れた問題です。
5. こちらも４同様、誘導に沿った丁寧な作業力と、前問と関連付けて考える力が問われた、まさに「ザ麻布！」問題です。ある程度時間をかけて丁寧に調べれば、（1）から（3）までで法則が見えてくるでしょう。その法則を使えば（4）が解けてしまうと言う問題でした。

　数年前まで見られた最後の難解な図形問題は近年出題されておらず、解きやすい問題が増えているため、捨て問はないと考えて対策をする必要があります。
　小4、小5の間は、標準問題はもちろんですが、時間をかけて試行錯誤する問題、具体的には、今年の入試問題の５のような、高度な知識がなくとも解ける入試問題にも親しんでおくことをお勧めします。また、その作業を楽しめるタイプなら、麻布の算数入試向きと言えるでしょう。
　小6の夏以降は、できるだけ多くの過去問を解き、麻布の入試出題者の思いを知ることが合格への近道です。入試問題は、「受験者に解いて欲しい」と言う、出題者の愛に溢れています。大問の（1）からは、（2）以降を解くためのヒントが伝わってくるはずです。麻布の先生からのラブレターに応える解答ができれば合格です。

武蔵中

　今年は、例年よりも「どこかで見た問題」が多かったようです。丁寧にミスなく取り組められれば、高得点は比較的容易でしょう。ただ、２のように小問の一問目を正解できないと、続く小問が解けないものもあり、点差が開きやすい問題構成です。全体の問題数が少ないだけに、条件の読み取りミスや計算間違いは致命的です。

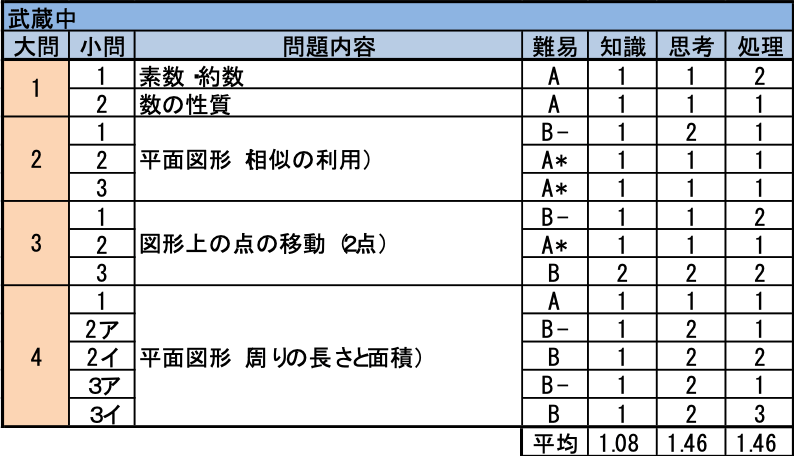
1. 典型題が並びました。ここは２問とも正解したいところです。
2. 相似の利用です。角度が等しいところから、直角三角形の相似に気づけば、楽に解き進められます。ただ、(1)を正解しないと、(2)(3)が解けず、しかも(2)(3)が易しいので、得点差が大きくなりやすい問題です。
3. (1)(2)は条件設定が複雑ではないので、図を正確に描いて調べれば正解できるでしょう。動点の出発時間がずれていることを読み外せば正解に辿り着きません。最初の方を読んだだけで「あの問題だ！」と思い込んで解き始める受験生をふるいにかける問題です。(3)はこれまでの演習量に左右される問題です。類題を取り組んだことがある受験生は比較的楽に解くことができたでしょう。
4. 一見オリジナリティを感じさせる問題ですが、設定自体は見慣れたものであるはずです。場合の数については図の成り立ちをしっかり理解した上での丁寧な作業が必要ですので、完答はしにくいでしょう。それ以外はしっかり得点したい問題です。

　今年はやや易しい印象がありましたが、今後も出題形式は変えずに、校訓通り「自ら調べ自ら考える」出題を続けていくことでしょう。一時期、相当に易化した時期がありましたが、ここ数年は受験生に見合ったバランスのとれた出題となっています。闇雲に難度が高い問題が少なく、受験生が取り組んできた学習内容を土台にしながら、柔軟な思考力や粘り強い作業力を必要とする良問が出題されます。そのため、算数は他の科目に比べて合格者平均点と受験者平均点の差が特に大きく、合否を大きく左右しています。
　こういう出題に対応するためには、４、５年生のうちから、塾のカリキュラムを丁寧に取り組み、こだわりを持って「なぜ？どうして？」を考える練習を積み重ねていきましょう。典型題の習得は不可欠ですが、パターンの丸覚えだけではなく、解法のポイントや問題の成り立ちを入手することが大切です。また、答えの〇×だけではなく、解答に至るプロセスを残しながら（手を動かしながら）学習することが必要になってきます。
早いうちに上記のような丁寧な学習方法が確立できれば、６年生では取り組む問題レベルを上げていくだけで、それ以外の特別な対応は不要です。しかも、６年２学期以降の過去問演習がとても効果的なものになるでしょう。
　出題分野は大きな変動がなく「比・割合」「平面図形」「速さ」「数論」の比重が高いことが特徴ですので、これらの単元については苦手意識を持たずに済むようしっかり学習したいところです。

桜蔭中

　桜蔭の算数と言えば、一読しただけでは理解できないような長く複雑な問題文や、非常に厄介な計算を大きな特徴としてきましたが、今年はふたを開けてみれば、面倒な計算が全くないという異例の年でした。高い読解力を求める「桜蔭らしい」問題はⅣに健在ですが、例年とは異なり、状況さえ理解できれば短時間で処理できる単純なものだったため、全く理解できずに0点で終わるか、全問正解するか、両極端な結果となった可能性があります。
　例年と比べると処理量が減った分難易度が下がり、読解力次第で高得点も狙いやすかったといえます。

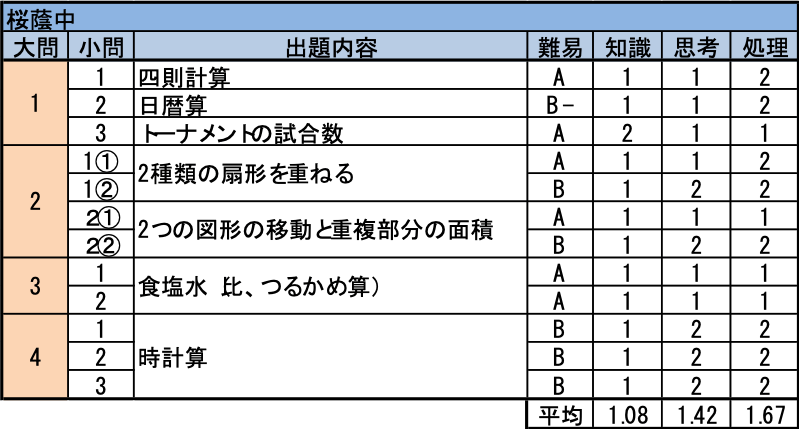
1. 従来は(1)で四則混合の計算問題と逆算が1題ずつ出題されるのが定番でしたが、昨年は逆算1題のみ、今年は計算1題のみの出題でした。(2)では昨年に引き続き暦に関する問題が出題されましたが、これには細かい点にちゃんと気をつけて解き切る力があるかどうかを試そうという出題意図を感じます。暦に関する様々な問題を練習しておくとよいでしょう。
2. (1) 緻密な思考を求めるという点で、②はとても桜蔭らしい問題です。全体を通じて一番厄介で、時間がかかる問題でした。桜蔭対策の練習にはもってこいの問題ですので、是非時間を計って解いてみましょう。なお、全てののりしろの大きさを同じにすることは求められていないので、どれか1～2枚で調整すると簡単に処理できます。(2) 素早く適切な図を描けるかどうかが勝負の分かれ目です。これは一朝一夕に身につく能力ではありません。早い段階から図を描く習慣を身につけましょう。①のような問題は大抵の場合、その後解き進める上でヒントとなるので、図を描きましょう。①の後、重複部分がどのように消えていくのか丁寧に考えて下さい。②の後半は、日頃から作図を重ねていれば、どういう場合に五角形ができるのかピンとくるはずです。
3. 本当に桜蔭の問題なのか目を疑ってしまうほどの基本問題でした。(2)は、わざわざ水そう③を使っているという問題の流れから、(1)で出た答え（Aが200g）を使うのだと判断してしまえば、つるかめ算の典型問題です。
4. 長く複雑な説明を、じっくり読んで考えることを求める点で、極めて桜蔭らしい問題です。問題の意味が分からず面食らった受験生も少なくないでしょうが、落ち着いて状況を把握すれば、針の動く角度が普通の時計と違うだけで、普通の時計算と同じように処理できることに気づきます。状況を全く理解できずに無得点に終わるか、楽々と全問正解できるか、両極端の結果になりそうです。

　冒頭で述べた通り、今年は例年とは異なり、厄介な計算が必要となる問題が出題されませんでした。しかしこれが今年限りの例外である可能性がある以上、桜蔭対策には計算の訓練が欠かせません。それも、相当のスピードと正確さ、そして自分の計算力に対して揺るぎない自信を得るほどの猛烈な訓練です。というのは、中途半端な計算力では、「計算間違えたかも…」と思えてしまうような答えが正解である場合すらあるからです（例えば昨年のⅣがその例です）。早い段階から計算力を磨き続けましょう。
　計算力以上に求められているのが、最後まで丁寧に考えを積み上げる力（今年のⅡ）、長い問題を読んで情報を整理し、理解する力（Ⅳ）です。例年よりも問題文がさらに長くなったことからも、これらの能力は今後ますます重視される可能性が高いです。従って、4年生から5年生にかけて一通りのテクニックを修得した後は、ⅡやⅣのような問題を丁寧に解き切る練習を重ねましょう。

女子学院中

　構成は大問が６。難易度は過去2年に比べて大きく上昇し、まさに御三家の一角らしい問題が並びました。一昨年、昨年と得点のしやすい問題が続いていましたが、そのレベルに合わせた対策では不十分であったでしょう。高い処理能力のみならず、深い思考能力も求められる出題となりました。短い時間内にこれだけの問題を全て解ききるのは難しいため、大問３、４、５の中での問題選択が鍵であったと言えるでしょう。

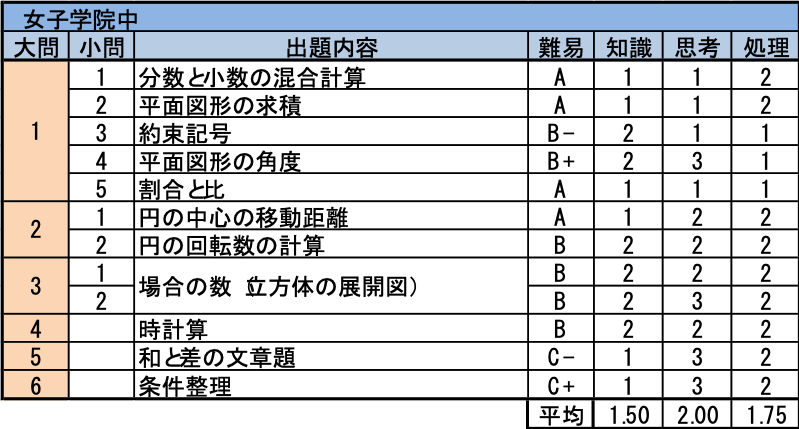
1. （1）（2）（3）（5）は女子学院受験生であれば簡単に解けるレベルの小問です。しかし（4）の平面図形の角度を求める問題は図が込み入っていて、角度を求める難問に慣れていないとすぐにはアイデアが浮かばなかったかもしれません。
2. 円の中心の移動距離と円の回転数の問題。（2）は応用の要素もありますが、難しくはありませんでした。
3. 立方体の展開図。11種類の展開図を覚えていることは必須でしたが、覚えていてもなかなか正解するのが難しかったと思われます。
4. 時計算の応用問題。類似問題を経験していないとすぐには解法が思いつかない可能性もあり、角度は出すことができても、時刻を出すことが若干難しかったでしょう。
5. 和と差の文章題。問題文の意味を読み解いて、通常の和差算のように考えることができれば正解できますが、時間に追われる中で冷静に解法を思いつくことが出来たかがどうかが分かれ目です。
6. 一見どうということのない問題に見えて、高度な条件整理を必要とするなかなかの難問です。ここまでたどり着いた受験生は少なかったのではないでしょうか。

　女子学院中の算数では問題文を読みながら同時進行で考え、読み終わった段階ですでに方針が立っているというような頭の回転の速さ、もしくは要領の良さが求められます。短い試験時間であるにも関わらず問題数が多く、思考の深さも処理能力の高さも必要で、じっと考えるというよりは、読みながらすぐに手を動かし図式化できる行動力も必要です。また、答えを出せれば何でもよい、という勉強の仕方ではなく、一度自分で正解できても解説を読むなどして他の解法も習得し、本番では最短の方法で解き進めるような訓練をしていきましょう。
難問に多くあたって自分の引き出しを増やすこと、ある程度のレベルまでの問題は時間を区切ってなるべく速く正解を出す練習をすること。このどちらも並行して学習を進めてください。
　さらに、女子学院の算数で必要な“スピードと正確さ”のためには絶対に欠かせないのが計算力です。計算をいかに工夫して要領よく正確に最短でこなせるか、は算数で高得点を目指すにあたって非常に重要なポイントになります。6年生になってからではなかなか自分のスタイルを変えられないものです。4年生、5年生の段階から計算の工夫を常に意識して練習を重ね、数に対する感覚を高めて下さい。そして5年後半からは、細切れに式を立てるのではなく一気に式を立て、分数を駆使しながら上手に計算をこなすことができるように計算力を鍛え上げましょう。
毎年出題されている平面図形の角度や求積に関しては、図中に情報を書き込む習慣をつけ、様々な問題を解くことで糸口を見つけるためのスピードを身につけましょう。
　突破口が見つけにくいような難しい求角や求積の問題でも、いくつかの押さえておくべきコツがあります。ここではそれはスペースの関係上割愛しますが、演習量を増やし、
女子学院の平面図形の対策はしっかりと講じて下さい。

雙葉中

　ここ数年の出題傾向通り、大問５題の構成は変わりませんでしたが、昨年一度姿を消した四則計算問題が再び出題されました。逆に、25年度以降（29年度を除く）出題されていた立体図形の問題がなくなり、同様に毎年出題されていた「速さと比」の問題もなくなるなど、出題分野の多少の変化が見受けられました。総合的には際立って難問と思われる問題はなく、標準レベルの問題が中心の出題でした。

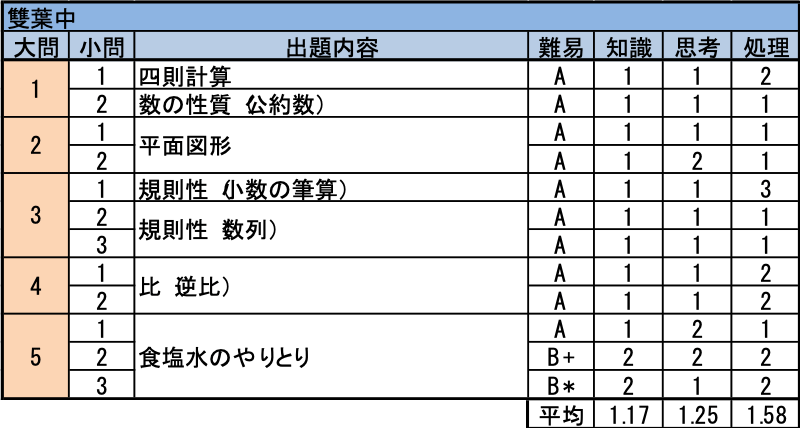
1. 四則計算と公約数の、確実に得点したい問題です。
2. 平面図形の問題ですが、基本問題です。（1）は面積の求積です。特に難しい計算はなく、確実に得点したい問題です。（2）は（1）で求めた正三角形の面積がヒントになります。正多角形の性質に慣れておくことも欠かせません。
3. 規則性の問題ですが（1）は小数の第８位まで求める４けた÷４けたの筆算。基本計算問題ですが、（1）の答えを（2）（3）で利用する問題ですので、計算ミスできない問題です。位を揃えて正確に早く計算することを日ごろから練習しておくことが大切です。
4. 畑の面積比と収穫量の比が逆比になることを利用して解く比の問題。（1）（2）ともに基本問題ですが、（2）は単位の換算に気をつける必要があります。
5. 塾のテキストでは定番の食塩水のやりとりの問題。落ち着いて状況を整理すればこれまで学習した手法で解決できます。(2)よりも(3)が取り組みやすく、(2)ができれば一気に最後まで進むことが可能です。

　今年は、総合的に難易度が下がった印象でした。特に、これまで出題必須単元のであった「速さと比」が出題されず、同じく「平面図形」「規則性」「場合の数」においても、基本問題が中心でした。また、「○○算」といったいわゆる中学受験算数の特殊算の知識を活用しなければならない問題はやや影を潜め、むしろ数の性質や多角形の性質など、基礎力を問う傾向に比重が置かれたようです。
　中学受験の学習スケジュールを考えた場合、４年生の段階では、まずは「正確な」計算力を鍛えることが必須です。数字・位取りを正確に書くなど、計算ミスをなくす練習が大切です。その上で、計算スピードを上げることを目指しましょう。注意したいのは、やみくもにスピードを求めないようにすることです。まずは徹底して正確な計算練習、その上でスピードを上げる練習をして下さい。
　次に、５年生では多くの塾で「速さ」「割合」「比」及び「平面図形」「立体図形」の基本を扱われます。今年の雙葉中のように、難関御三家とは言え、基礎力重視の問題を中心に出題されることもあります。５年生では、入試必須単元の基礎力を徹底的に磨き上げて下さい。その際に大切なことは、線分図や図をかき、手を動かしながら考えることです。「○○算」のパターン解法に慣れてしまった受験生ほど、試行錯誤しながら考えることが苦手になる傾向があります。フリーハンドで素早く線分図や図をかき、頭の中を整理しながら考える試行錯誤力を、５年生で身につけることを意識して下さい。
　そして、６年生では入試本番を想定した「速さと比」「割合と比」「図形と比」など、組み合わせ問題が目白押しとなります。発展レベルの問題になると、問題文を読んですぐに解法が分かる単純な問題はなかなかありません。その際に効果を発揮するのが手を動かしながら考える試行錯誤力です。それは同時に、解答用紙に考え方を書かせる問題への対策にもなります。雙葉中学校においては、再び難易度の高い問題が出題される可能性は十分に考えられます。発展レベル問題までしっかりと対応出来ることを目標にして下さい。
　また、過去問に取り組む際は前半が難しく後半が易しいパターンもあるので、前半の難しい問題に必要以上に時間をとられると後半の簡単な問題に手を付けられなくなってしまう可能性もあります。初見の問題でも「すぐ解く」「あとでゆっくり考える」をすぐに判断できる時間配分の練習をしておくことをお勧め致します。

筑波大付属駒場中

　調べ上げやそれを通じた発見的考察など、その場での作業に重きを置いた出題が続いています。ここ数年は過去に比べれば控えめの作業量、難易度の問題が続き、40分という短い時間に見合った問題でしたが、今年は再び以前のように難しい問題が随所に見られ、首都圏最高峰の決戦にふさわしい厳しいセットとなりました。

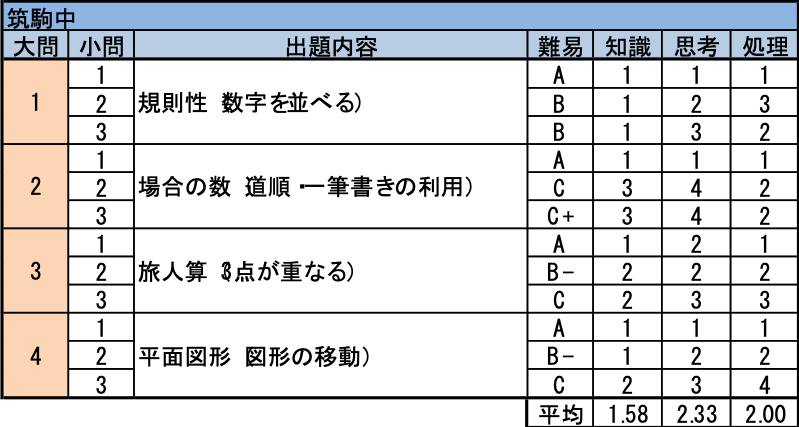
1. 規則に従って立てられた旗の位置について考察する問題です。特別な考え方は全く必要としませんが、短時間で緻密に追跡し切ることが求められています。
2. 同じ道を何度か通って元に戻る道順を考える問題です。(2)以降は単純に調べようとすると難しく、一筆書きのルールとの関連性を考えることで糸口が見えてきます。
3. 3点が重なるタイミングを見つける問題は経験があるでしょうが、(3)は直線上を1点のみが往復するという味付けが加わっており、しかも単純に調べるには大変な数値設定となっています。
4. 円の内部を三角形が転がる設定は平成7年にも出されており、(2)までは難しくありません。(3)では点Bの軌跡が三角形ABCから一部はみ出すことに注意が必要です（なぜ2.6㎝が与えられたかと考えるとわかります）。その後の数値計算も煩雑で、よくあるタイプに見えて正解しにくい問題といえるでしょう。

　筑駒中は国立ということもあり、中学受験独特のテクニックを必要とする問題はまず見られませんが、その代わりに緻密な作業や規則の発見といった、現場での作業力が重視される問題が出されます。受験者レベルを考えると標準的な問題を確実に押さえた上で、さらに難しい問題の一部にも食い込めないと合格は厳しいでしょう。
　そのためにはまず小さいころからの「ああでもない、こうでもない」と試行錯誤する習慣が土台として必要です。幼児期から一方的に教わり続ける学習を続けていると筑駒中からはどんどんと遠ざかる一方になります。
　また塾での平常の学習において、テクニックを覚えて使いこなすだけの学習は併願校対策にはなっても筑駒中には無意味です。しかしなぜその方法で解けるのかといった点からきちんと理解しておくことで、その考え方が活かされる問題も出されるので、「なぜ」という点にも関心を持って学習を進めていきましょう。
　さらに過去問対策においては、40分という短い時間で得点を最大化する練習が必要となります。最初は「時間をかけて解けた」でもよいですが、作業を効率よく行う工夫、よりよい着眼点といった時間短縮につながる方法にも気を付けながら学習するようにしてください。また大問ごとに後ろに行くほど難しくなることが多いですが、どの大問が取り組みやすいかは必ずしも決まっていないので、どのタイミングで見切るかという問題の選択にも気をつけるようにしましょう。

駒場東邦中

昨年に続き、やや難度を抑えた問題構成で、手も足も出ないような超難問は見当たりません。今後もこの辺りの出題レベルでとどまるかどうかはもう少し慎重に推移をみる必要はあるでしょう。しかし、この学校の定番とも言える出題傾向である「数」と「図形」の出題は、受験生が比較的手を出しやすいレベルにすることで、選抜試験としての完成度が高くなっているとも言えそうです。

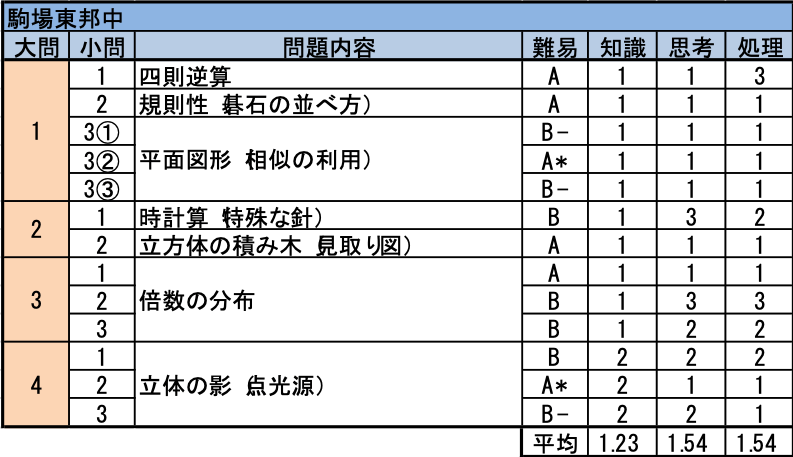
1. (1)の計算問題と(2)の規則性の基本問題の２問は落とすわけにはいきません。(3)は相似の問題ですが、中点の利用に気づけば①は正解できます。①を正解できると②③は簡単ですので、点差は開きやすいでしょう。
2. (1)は時計算の基本的な考え方で解けますが、針の特別なデザインで、作業力（図を自分で描く）が必要な良問に仕上がっています。平面図形の性質を利用して角度を求めるところなど、難問ではありませんが、差がつく一問でしょう。(2)は最近の駒場東邦らしい出題です。立方体の積み木の見取り図を描くのですが、この学校の受験生レベルに対しては易しく、もう少しひねりがある方が差がついたかもしれません。
3. 倍数の分布の問題です。「割り切れない」を太字で強調してありますが、少々題意が読み取りにくい問題だったかもしれません。問題自体は、倍数の個数や周期性などを組み合わせた良問です。作業量が多めですが膨大でなく、小問３問ともしっかり得点したいところです。
4. 点光源による四角すいの影の問題です。この問題も(1)が解ければ(2)は易しくなるので、点差が開きやすいです。(3)は(2)までが解けなくても解答可能ですが、最終問題でしたので試験時間との勝負になったかもしれません。

　思考力や作業力を問う問題が多く、数学的背景を交えた出題も例年多く見られるので、パターン学習の積み重ねだけでは、高得点は難しいでしょう。ただ、合格点に届くためだけなら、処理が面倒なだけの平易な問題も出題されるので、「取りこぼしを最小限にする」ことが攻略のポイントになるはずです。
　４、５年のうちから難問にあたることは必要ありませんが、テスト対策だけの勉強に陥って丸覚えの学習になることだけは避けなければいけません。たとえ典型題であっても、問題の成り立ちや仕組みに目を向けて、丁寧に取り組み続けることが大切です。図や表を自分で描いたり、書き出して調べ上げたりする経験をたくさん積み重ねましょう。
　６年に入ってからは、日頃から難度の高い問題に対して、あきらめないで粘り強く解き進める練習が必要になります。記述対策として、丁寧に書き出したり、図や表で調べ上げたりする作業は続けて取り組んでください。また、一通りの解法ではなく別解を考えることで、適切な解法選択やアプローチの引き出しを増やす効果が期待できます。解くスピードだけにとらわれるのではなく、じっくり深く考える習慣が大事です。

渋谷教育学園渋谷中

　数年前までは後半の大問を中心に高度な情報整理力や作業力が求められるなど共学校としては最も難しい問題を出す学校の１つであり、６割とれれば十分とも言われていました。その後は前半の小問集合を中心に典型題が増えたことで段々と得点しやすい状況となり、今年はついにすべての問題が標準レベルまでに抑えられたため、６割では合格がおぼつかなかっただろうと思われます。

1. 小問集合ですが、これまで見られなかったような基本的な問題も混じっています。ここは全問正解すべきです。
2. 立体切断ですが、渋渋の大問としては異例なほどオーソドックスです。(4)の2回切断で差がつくかもしれませんが、渋渋受験生であれば正解したい問題です。
3. 「マイナンバー」を題材にしていますが、規則通り計算すればよいです。(4)は2年連続の理由説明問題ですが、主張が正しくないことを説明するには成り立たない例を1つ挙げるだけでよいことがわかっていれば(3)での考察がそのまま答えになります。
4. 図形の回転移動に関する標準的な問題です。(2)(3)の途中過程について「図をかくこと」「それぞれの式が図のどの部分のものかわかるようにすること」と指示が明確であり、書きやすかったのではないでしょうか。

　数年にわたり易化傾向にありましたが、さすがに今年の問題は行くところまで行きついた感があります。来年は反動で難しくなる可能性もありますが、それでもこれまで同様１の小問集合を中心に、塾での類題経験があるような解きやすい問題が混じるものと思われ、まずはこれらを確実に正解することが大切です。特に易しかった今年こそこの点が重要だったといえます。6年の前半まではこのような普通の問題を確実に正解できるよう取り組んでいきましょう。これは応用問題を考えるための土台にもなります。
　来年は再び難化する可能性も想定しておきたいところです。主に後半の大問で難しい問題が出る場合が多いですが、頻出テーマは「速さ」などの込み入った設定で条件整理が必要な問題、「場合の数」では丁寧な場合分けや調べ上げを要する問題、「図形」では移動や立体切断などの作図力が求められる問題などです。
　これらの問題に対しては与えられた条件や思考している内容をきちんと整理しながら進めることが大切であり、そのためには自分の考えている内容をわかりやすく残しながら進めていく学習が有効になります。渋渋中では一部の問題で途中過程を記述させていますが、今年の４の指示は途中過程の書き方のみならず、思考を整理するために何を残すとよいかという点も示唆してくれています。すなわち、それぞれの式・計算で何を求めたのかを１つ１つ明確にしていくことが答案をわかりやすくするだけでなく、自らの思考を整理することに大きな効果をもたらすのです。過去問に限らず入試レベルの応用問題に取り組む際には、この点を意識しながら取り組むようにしてください。

豊島岡女子学園中

構成は例年通りの大問６題で、前半から後半に向けて難易度が上がっていく形でした。非常に解きやすい大問１から始まり、豊島岡を目指す生徒ならば解けなければならない大問２と３、そして深みのある大問４・５へと展開し、大問６に立体図形の難問が出題されるというスタイルもこれまでと同じでした。頻出の平面図形の相似や速さの応用問題は出題されませんでしたが、全体的に、今年度はこれまでよりも時間のかかる難問が多く出題され、第一回試験の合格者平均は66.9点と例年よりやや低めでした。

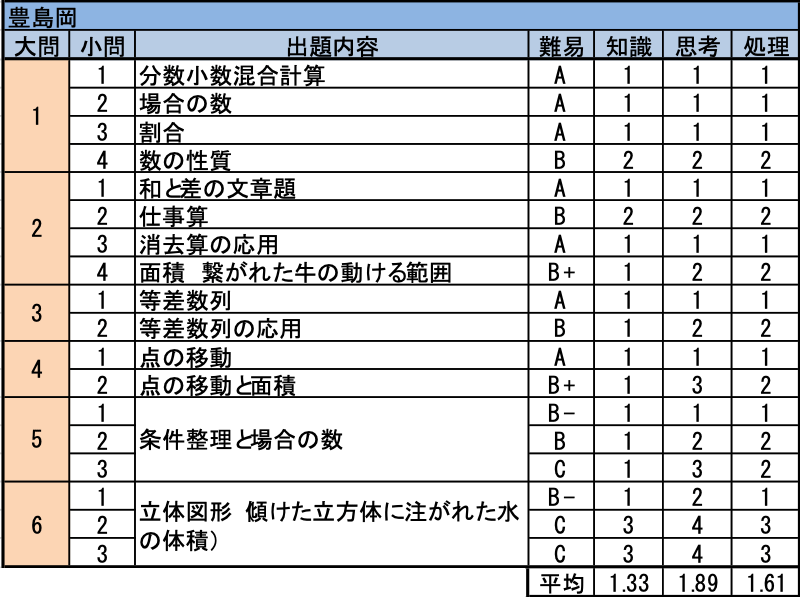
1. 計算１題と小問3題。(2)は2017年度の大問1(2)と同じ問題です。
2. (1) 和と差の文章題。問題の意味を考えればすぐに解けるはずです。(2) 与えられた条件を整理し、数に置き換え、正確に処理する能力が問われます。(3) 文意の通りに式を立てれば後は消去算で解くだけの平易な問題です。(4) 作図をする際に頂点同士の距離が大きく関係することに早く気付くことが必要です。
3. (2)は独特な規則性をいかに早く発見し正確に計算するかがポイントになります。
4. (2)は２つの面積を時間ごとに書き出すなどして規則性を察知できるかどうかが鍵です。
5. (2)と(3)は勝ち負けがついた場合とあいこの場合には二人の位置関係はどうなるかを分析してから解けば両方とも答えを出すことができますが、力づくでやろうとすると(3)は時間もかかりますし、正解を出すのは難しくなるでしょう。
6. 例年通りの立体の難問です。(1)は解けなければなりませんが、(2)と(3)は傾けた立体に注いだ水の体積を求める問題で、イメージすることも難しく解けた人は少なかったでしょう。

　豊島岡女子学園中では、前半の大問１と２及び３ 以降の(1)は必ず得点し、大問３以降の
(2),(3)をいくつ解けるかが勝負になります。前半及び後半の(1)には、立ち止まらずに解き進めたい問題が例年出題されていますが、全てが受験生全般にとって易しい問題というわけではなく、いくつかは　「豊島岡を目指す受験生にとっては」易しいレベルの問題です。ここで確実に得点できるためには当然基本から応用までの考え方が全て習得できていて、どんな言い回しをされてもすぐに対応できる力が必要となります。言うまでもなく、軽微なミスは命取りになります。
　後半の(2)以降では、豊島岡らしい問題が並びます。今年も一見するとすぐに解けそうに見えて解き進むと意外と複雑であった、という問題が出題されましたから、時間をかける問題の選択に迷ったり、解き始めたものの上手く答えが出せずに次の問題に乗り換えたりした受験生は多かったのではないでしょうか。
　豊島岡の対策としては、範囲に限らず、基本から叩き上げたオールマイティーな力をつけるために問題数をどんどんこなしていくこと、そしてある程度までの問題であれば問題を読んですぐに解けるというスピードをつけることが大切です。前半の問題をいかに速く正確に解き、後半の問題に取り組む時間を確保するか、が合格点を取るための前提条件となってくるからです。そして、良く練られた発展問題が出題されますから、難易度の高い問題にもじっくり取り組む時間を5年生のうちから取り、できるだけたくさんの良問難問に挑戦したほうが良いでしょう。
豊島岡の算数では、出たとこ勝負でセンスで解くことや、とにかく書き出して力尽くで解く、というやり方では合格点はとれません。その場で手を動かして根拠のある解き方を探し出し、根拠のある書き出しを行うというような、これまでの知識と経験に基づく確実な方法をとることができる力を養いましょう。
　特に対策を取るべきテーマとしては、立体図形、条件整理と場合の数のミックス、速さ、割合です。これらは頻出です。特に立体図形では問題の意図に沿って作図しイメージを的確に把握する能力が必要となります。問題に図が載っている問題においても、まずは自分で作図してみるなどして立体の感覚を身につける練習を重ねましょう。
豊島岡の算数で合格点を取るには、基本からの徹底的な習熟、問題の意図を理解するまでのスピード、立式と計算の正確さ、難問を楽しんで解く探求心。これらが必須です。

早稲田中

　例年に比較すると、今年はやや易しくなったように感じます。元々、見たこともない超難問が出題される学校ではありません。しかし、「一見、定番に見えるが、取り組んでみると、ひとひねりしてあって手間もかかる。」問題が、同じようなレベルで並んでいる出題形式が続いています。やはり今年も、ある一定の学力がないと、歯が立たない問題セットと言えるでしょう。

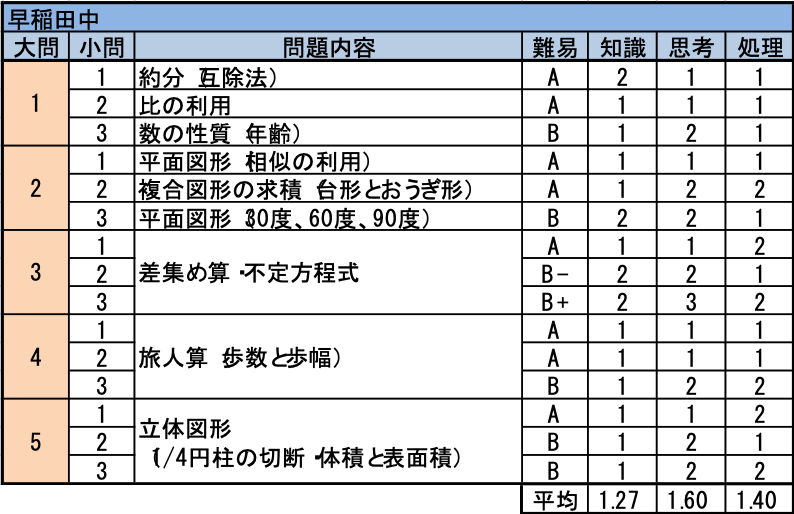
1. (1)大きな数の約分ですが、「割るときには差に注目する」鉄則で、比較的簡単に処理できます。(2)は比の活用の定番問題ですので外せません。(3)は十の位と一の位の差に注目できれば、あとは少し調べるだけですが少々厳しい問題です。
2. (1)は２組の相似を利用する全くひねりの無い典型題です。(2)はおうぎ形が見えるので、「中心と円周上の点を結んで考える」ことができれば正解に至ります。３：４：５の直角三角形を利用する生徒もいたことでしょう。(3)は正三角形の角度や折り返しに注目し、最後は頂角３０度の二等辺三角形の求積に持ち込める定番問題です。
3. （１）は差集め算の基本問題で易問です。(2)では(1)で求めた単価から、入れ替えによる代金の増減が分かりやすい数値なので、これも外せません。(3)は「１個落として１個もらった」ことを「１個だけ買い替えた」言い換えることで、代金の総額が３で割り切れる場合を見つけるだけです。１５個で２１８０円と分かれば正解は目の前です。
4. 条件に歩幅と歩数とありますので、状況図（速さの線分図）が思い浮かびますが、ダイヤグラムの方が処理しやすい問題です。兄の歩数の様子で必要な数値が見えてきます。小問３問とも正解したいところです。
5. (1)円柱の切断なので、一瞬驚きますが、切断部分は定番の三角すい台です。立体の切断に慣れている生徒であれば、正解に至るのは容易でしょう。(2)表面積については、切断面（△ＦＰＲ）の面積が分かるとすれば、塾で扱ったはずのあの問題が必ず思い出されるはずです。最後の問題ですが、解きやすい一問と言えるでしょう。

　ここ数年受験者平均点は５割を切ることが多く、４割を切ることもあるほどです。今年は易し目でしたが、受験者レベルに対してやや厳しめの出題がこれからも続くことを想定した対策をしておきたいところです。「図形」、「速さ」、「比と割合」、「数の性質」は頻出分野です。
　４、５年のうちは塾のカリキュラムに沿って、偏りがでないようにまんべんなく学習しましょう。入試では短答式の解答記入なので、答えの〇×だけに気を向けがちです。しかし、解く過程をおろそかにすると正解に辿り着けず、短答式である以上途中点や部分点はありません。解き始めから解き終わりまでの流れを丁寧に取り組む学習を習慣付けることで、正答率を高めることを心掛けましょう。また、日々の計算練習や、答えを記入する前に必ず問題文を確認する習慣など、ミスを減らすための基本動作の徹底が不可欠です。
　６年生では、特に「速さ」と「図形」の問題は最重要です。「速さ」では、状況図だけでなくダイヤグラムにも慣れておくこと、「図形」については平面図形、立体図形を問わず、充分な演習量が必要です。塾のテキストに掲載されている難度の高い問題まで数多く解いてしっかり慣れておきましょう。問題を解く力を高めるとともに、難易度順に並んでいない出題に対して、解くべき問題を見極める目も養えるはずです。

早稲田実業中

　例年、早実中では①大半の受験生が解けるような易しい問題、②スタンダードな問題、③試行錯誤しつつ解法を探さねばならない難問、の3つのタイプの問題が出題され、①と③の間で難易度に著しい乖離がありました。受験者平均点は毎年50点程度ですので、①の全てと②の大半を押さえれば合格点に達したと考えられ、この点で、算数があまり得意ではない生徒も意外と狙いやすい学校でした。ところが今年はタイプ③の問題の難易度が大きく下がり、ほとんど②に近づきました。③がいわゆる「捨て問」ではなくなったことで、平均点は例年より上がったものと思われます。そのため、③のタイプを苦手とする受験生は不利になり、これまで以上に②の取りこぼしを減らさないと合格点には届かなかったと考えられます。

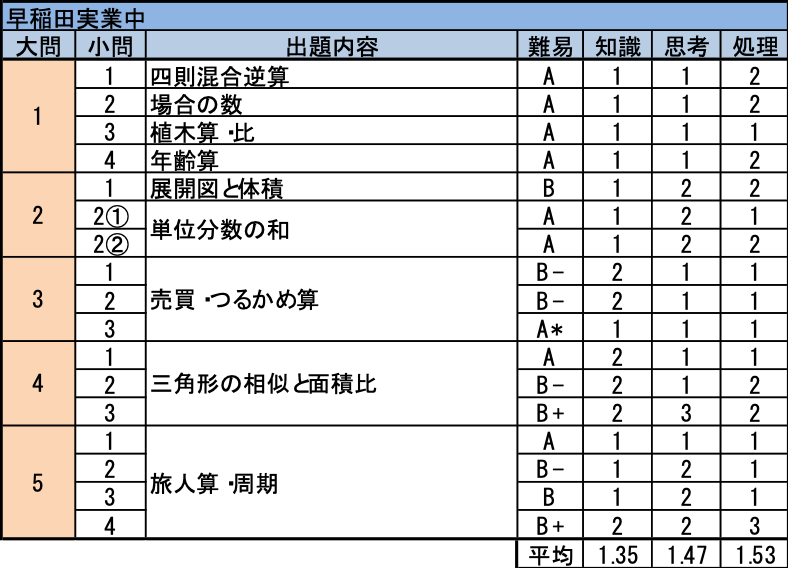
1. どれも塾で扱われる基本問題ですので、全問正解が望ましいです。
2. (1)は立体が苦手な受験生には難しかったかもしれません。(2)のような見た目の問題は嫌われる傾向がありますが、実は「手順」の通りに作業するだけのボーナス問題でした。
3. 問題文は長いですが、ほとんど利益についての説明しか書かれていないので、状況を整理するのは難しくありません。この問題を解けないと合格は厳しそうです。
4. (1)は有名な問題ですので、(1)に着手した多くの受験生が適切な補助線を引いて正解できただろうと思います。(2)は是非修得しておきたい問題です。(3)は少し難しめですが、難関校対策を重ねてきた生徒であれば、似たような問題を解いたことが何度もあるはずです。
5. 冒頭で述べたタイプ③に該当するのがこの問題ですが、例年と比べるとはるかに簡単で、書き出し作業もほとんど不要なため、十分に得点を狙える問題です。少なくとも(1)は簡単に求められるので、(1)だけでも解いておきましょう。(2)以降は、Pの移動角度に着目すればよいことと、PとQが、出会い→追い越し→出会い→追い越し… をくり返すことに気づけば簡単に解けます。

　塾で上位のクラスに所属し、授業とテキストをしっかりこなしていれば、「見たことがあるぞ」「これならできそうだ」と感じるような問題が多く、それらをしっかり得点できれば恐らく合格点に達すると考えられます。
１では、4年～5年のテキストで基本問題として扱われるような非常に易しい問題が出題されています。4年、5年でしっかり基礎を身につけましょう。
　6年生の1年間は、「見たことがある、解けそうだ」と感じられる問題を増やすべく、各単元の応用問題を一通り解くとよいでしょう。
普通の問題を普通に解ければ合格できるという傾向が続きそうですが、今年、タイプ③の難易度が大幅に下がったことには注意が必要です。いわゆる「捨て問」をなくすことで、難しめの問題をちゃんと解ける子が選別されるようになる可能性があります。試行錯誤しつつ正解に辿り着くことが求められる問題は、短期間で解けるようになるものではありません。すぐに諦めて答えを見るのではなく、ああでもない、こうでもない、と鉛筆を動かして考え続けた経験が必要なのです。時間に余裕のある5年生までの間に、じっくり考える練習を積んでおくとよさそうです。

慶應義塾中等部

　例年、標準問題が多い一方で、問題数が多く、出題分野も広範囲なため、素早く解法を思い出し、解く速さと正確性が求められる出題です。また、計算も、難しくはありませんが繁雑なものが多いです。今年も、ほぼ例年通りの出題でしたが、最後の７（２）は難問でした。他の問題でしっかり得点し、全体で9割を目標としたいところです。

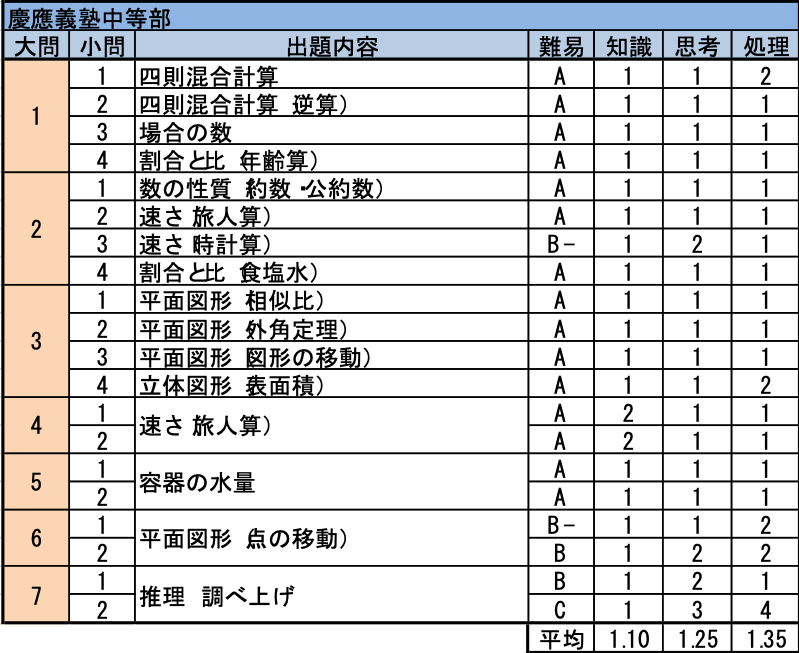
• １～３は、ほとんどの問題が、問題を見た途端、瞬時に解法を思い出し、手が勝手に動くくらいでなければ合格は厳しいでしょう。２の（3）の時計算は間違いやすいため、12時間で長針と短針が何周差になるかをよく考えましょう。３の（4）の立体の表面積を求める問題は難しくはありませんが、短時間で簡単に解いたかどうかがポイントとなります。
• ４は人と電車の速さを和差算で解きます。５は水の入った容器が、底面が変わることで、高さがどう変化するかと言う典型的な問題です。いずれも、時間をかけずにスピーディに解きたい問題でした。
• ６は動く点の問題です。グラフから2点P、Qの速さを求めた上で、長方形ABCDの縦の長さが求められれば準備完了です。後は素直に、設問通り解きましょう。
• ７は推理と調べ上げです。（1）は正解したいところですが、（2）を時間内に正確に調べ上げるのは難しく、時間が余った子向けのチャレンジ問題です。

　小4、小5のうちは標準問題でいいので、苦手単元を作らず、すべての単元の問題が確実に解けるようにすることと、計算が速く正確にできるよう、計算の工夫を常に意識し、日々の訓練を怠らないようにしましょう。
慶應中等部の解答は、全問答えのみの上、解答方式が特殊なため、小6後期以降の過去問演習では、必ず本番同様の解答用紙を準備し、その方式に慣れておく必要があります。また、過去問で正解した問題でも、より素早い解法を確認しておくことが重要です。
男子はもちろん、女子はより高得点での争いになります。問題を見れば迷わず解法が頭に浮かぶくらい演習を重ね、入試に臨むことが必要です。

渋谷教育学園幕張中

　例年通りの大問５題構成で、文章題は一見見慣れない設定でその場での整理力が試され、図形ではありふれた設定のようで補助線の引き方や組み合わせ方などの試行錯誤が問われたのもいつも通りでした。
　今年は文章題の設定は読み取りやすかったものの、丁寧に調べる力が例年以上に問われました。難問といえるのは立体図形の１問のみですが、その他でも容易に得点できる問題が少なく、受験者平均39.4点、合格者平均53.2点という厳しいセットとなりました。

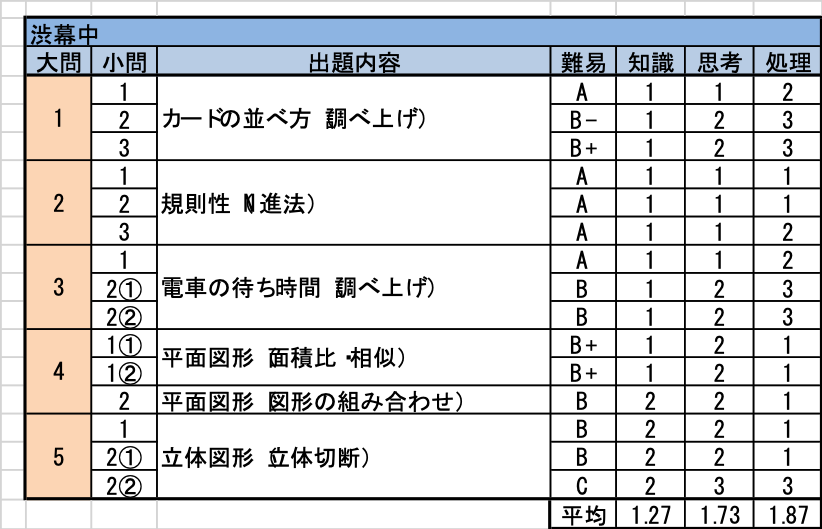
1. カード並べというありふれた設定ですが、2人の大小を比較するタイプは珍しく、「このあたりだろう」という見当付けと緻密な作業の両方が必要となります。
2. N進法の定番問題で、短時間で確実に正解する必要があります。
3. 電車の待ち時間に関する問題ですが、60分なのでいろいろと考えるよりも調べてしまった方が早いでしょう。
4. (1)補助線1本をうまく引けると相似の問題になります。(2)「1：2」「1：3」の直角三角形から「あの問題」を想起できればすぐです。
5. 恒例の立体切断ですが、側面が平行でない分難しくなっています。(1)では長方形を底面とせず、三角形を底面とした断頭三角柱と見ます。(2)②はそれ以前の設問がヒントになっていますが、体積比についての深い理解と思考を要する難しい問題です。

　渋幕中では定番パターンそのままの問題は少なく、条件整理や調べ上げなどその場での作業力が重視されます。とはいえ、今年の２のような定番問題そのもの、４(2)のような定型問題に結びつけることで解決する問題も一定数見られるので、標準的な解法については一通り身につけることが必要となります。
　塾では一般的に４、５年生がこのような解法の習得をメインに行う時期として位置づけられています。なので、この時期にはよく使われる手法はきちんと身につけるようにすべきです。しかしパターン習得一辺倒ではなく、応用問題にも取り組み、手を動かしながら「ああでもない、こうでもない」と試行錯誤する時間もとるようにするとよいです。その際に解けなかった問題を覚え込むように繰り返すことに意味はありませんが、解説などからよりよい整理方法などを吸収することは有用です。
　6年生になると志望校対策が本格化します。塾のテキストにそのままあるような問題は少ないので、過去問などを通じて初見の問題への対応力をつける必要があります。
　文章題では「○○算」といった中学受験特有のテクニックに持ち込む問題は少なく、問題の状況を整理する、丁寧に調べ上げる、条件を満たす場合を見つけるといった作業力が重視されます。そのためには問題を「じっと見て」解法を引き出したりうまい方法を見出そうとしたりするのではなく、わかっていることを整理してみる、いくつかの場合を調べてみるというように「手を動かしながら」考えるようにすることが大切です。この力は解法の習得・引き出しをメインとする塾の普段の授業、テストだけでは十分に身につかないので、過去問などを通じて十分に練習するようにしましょう。
図形では、以前は渋幕特有の問題として作図問題があり十分な対策が必要でしたが、近年では相似・面積比や立体切断など塾で通常学習する手法を組み合わせることで解決する問題が中心です。しかし誘導が少なく、補助線を見出す必要がある問題が多いので、普段から塾のテキストに載っているような問題についても、もし誘導がついていなければどうするか考えてみるとよいです。
　渋幕の問題は難易度順に並んでおらず、所々に難問が含まれます。例年合格点は高くないので、試験時間内での取捨選択が大切です。過去問に取り組む際には問題の選択にも気をつけて練習するようにしてください。

聖光学院中

　例年通り大問５題構成で、「立体図形」「場合の数」「相似の性質」と聖光学院の頻出分野の大問の構成でした。立体図形の問題は聖光の顔になり、今年は難易度の高い展開図の問題も出題されました。また、論理と推理の問題、問題の理解・整理を必要とする出題も聖光の傾向であり、今年は時間（処理）配分が例年より合格のために重要な要素になりました。聖光学院の合格平均点が例年８０％ですが、より思考力、処理能力が求められる出題です。

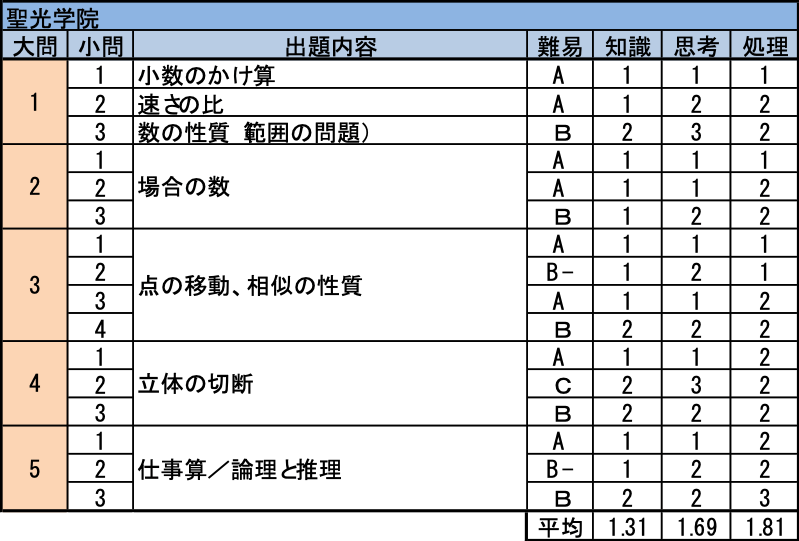
1. (2)の「速さと比」は確実に押さえたいところです。(3)の「範囲の問題（不等式）」は問題を理解し、整理していく能力が求められ、差がつく問題です。
2. (2)は調べ上げの問題で、確実に処理していくことがポイントです。（2）の処理でパターンが見えれば、(3)の素数が条件に該当しないことに気づきやすくなります。
3. 聖光で毎年出題される「相似の性質」です。正六角形の問題で、(3)(4)も難関校対策で解法を演習している相似の問題のため、合格のためには全問正解するべき問題です。
4. (2)のダブル等脚台形の切断の展開図は難問で、処理にも時間がかかります。むしろ、(3)の“共通体積を導く解法”で確実に得点していくことがポイントです。
5. 推理分野のゲーム理論の問題です。(1)の仕事算は計算ミスに注意 (2)は各人の時間単価を出すことを気づけば易しい問題です。(3)は最小値を求める推理問題ですが、各仕事に対する各人の優先する仕事を推理すれば、解答が導き出せます。

　聖光学院中は、合格平均点と受験者平均点の差が小さく、合格最低点も例年高い（８０％）特徴があります。問題のレベルは高いですが、塾の難関校対策クラスで一度は見かけたタイプの問題が多く、しっかり訓練した生徒には合格しやすい学校です。出題分野は聖光の顔になった「立体図形」、「平面図形（相似の応用）」「場合の数」「速さと比」「規則性」と例年決まっています。この点も勉強の比重をかけやすく、平均点が高い理由になっています。その傾向に準じながらも、今年の[1](3)不等式範囲の様な問題を理解・整理する能力、[5](3)「論理推理」の解法は最近の難関校の傾向問題もあり、より思考力、処理能力を求められてきています。
　「立体図形」「平面図形」では相似の解法を利用する問題が出題され、点の移動を絡めてくるのも特徴です。塾の上位クラスや難関校で過去出題された問題の解法の範囲なので、種々の問題を解いて、高度な解法を繰り返し演習し、身につけていくことが大切です。
「場合の数」「規則性」は知識、思考は難しくないですが、処理能力が大切で、書き出して素早く確実に計算していく練習も取り入れて、確実に答えを出していくことが重要です。
　「速さと比」は大問で長文出題される年もあります。問題を理解・整理（思考力）が重要なので、速さの長文問題を整理するトレーニングをしていくことは必須です。大問で出題されると点数に差がつく（大問の(1)が難しいパターン）可能性が高いからです。
聖光学院は塾の上位クラスでしっかり訓練をした生徒が合格に近い学校です。4年生～５年時は、塾の上位クラスを目指し、そのクラスを維持していくことを目標に、聖光の頻出分野での苦手を克服していくことがポイントです。特に、比の応用（倍数算）および相似の活用、場合の数・規則性における正確な書き出し、速さにおけるダイヤグラムの考察等は演習しておく必要があります。６年生の前半（夏休み終了）までに頻出分野は得意分野にして、問題文を見て知識の選択、思考による方向性を見分けられる能力をつけます。６年後半に聖光学院対策、他難関校の過去問で演習して、高度な解法を確実に定着していきます。特に、今年の［５］のゲーム理論の問題は、他の難関校でも最近出題傾向の高い思考力を問う問題で、今後も出題が予想されるので、十分な対策が必要です。

栄光学園中

　例年通りの大問４題構成でしたが、例年出題されていた「数の性質」が出題されず、「図形の移動」が３年ぶりに復活して、根拠が問われる記述も式と考え方になりました。栄光の特徴であり、難問である「調べ上げの問題」も、今年は表の整理、規則性により解きやすい問題になりました。一方、今年は規則性を見出して論理的に解く総合問題が出題されて、今後の栄光対策の指針となる良問でした。今年の合格平均点は４９点（７０％）で、例年より高かったですが、同様に易しかった2016年（５７点）より低く、受験生に差をつけるには適当な問題構成になったと思います。

1. 正六角形内の移動で移動角度は解りやすい問題です。(2)は誘導があり、式または考え方も答える点数配分も高い問題です。この大問は確実に得点したいところです。
2. (2)は立方体の例示もあり、立方体の展開図のパターンを覚えておけば解きやすい問題です。(4)も正十二面体の展開図を視覚で覚えれば答えは導き出せます。
3. 以前難関校でよく出題されたオセロの問題です。調べ上げ問題ですが、表にすれば確実に解ける問題です。(4)の黒の最大、最小の問題も(2)、(3)の処理でのパターンを規則性として捉えれば正答を得られます。
4. 論理推測、規則性のツールを使って解いていく総合問題です。(2)①はつるかめ算と不等方程式、②は論理推理、(3)は規則性からの調べあげを解法にすれば、栄光学園の受験生なら容易に解ける問題です。

　栄光学園中は、合格平均点と受験者平均点の差が大きく、合格最低点も例年は60％～65%が中心でした。その理由は、栄光の特徴である「調べ上げの問題」の処理能力が難解で、時間配分が受験者にとって課題になるからです。しかし、2017年、2019年は調べ上げの問題も規則性（パターン）を取り入れ、塾の難関校（栄光）対策クラスで習う範囲の問題になってきました。そのため、調べ上げは最小限になる様に、予測を立てて、規則性を見出していくことが解法の王道です。
　今年は出題されなかった「数の性質」も栄光の特徴であるストーリー性の高い問題でしたが、今年はこのストーリー性は総合問題に継承し、栄光の良問として磨きをかけてきました。「数の性質」「総合問題」の共通としてのツールは規則性の発見と論理推理です。このツールは他の難関校の必要な解法技術なので、十分に演習しておく必要があります。
　また、中堅校志望の子が苦手とする「つるかめ算の応用」「ニュートン算」「水量と体積」の分野の応用問題も出題も例年頻出で、この分野は確実に得点する必要があります。
　ここ数年は、「図形の移動」「展開図」の出題が目立ち、立体図形（展開図）、平面図形の配点が50%を超える年もあります。この分野の知識、思考力、処理能力を高め、５年生の時期に得意分野にしておくことが必要です。この分野における栄光学園の特徴は、4年生、５年生での知識の重要性が、他の難関校より高い特徴があります。出題傾向は、６年生で知識を伸ばしていく相似や点の移動は出題されず、４年生で習う「展開図」、５年生の「点の移動」が中心です。4年生、5年生で知識、応用力を完成させ、６年生で思考力を養成していく流れになります。
　また、調べ上げの問題は６年生になって時間をかけて演習出来ないので、5年までの間に時間をかけた訓練も必要です。6年では、夏休み前には過去問で弱点分野を把握し、他の難関校の類似問題で定着させて、塾の志望校対策で仕上げが出来るスケジュール感が理想です。
　栄光学園の今後の出題傾向ですが、「数の性質」の復活、「調べ上げ問題」の難化の可能性もありますが、今年の問題は受験生の思考力を判断するには理想的な問題構成だったと思います。論理的推理、規則性の応用は、現在の難関校の傾向であり、栄光学園合格のためには難関校（特に、麻布、武蔵）の同じ傾向の問題を演習し、常に思考力、処理能力を高めていくことが重要です。

浅野中

　昨年同様、大問５問構成でしたが、毎年出題されていた速さの問題が姿を消し、総合的に、難易度がやや下がったような印象でした。ここ２年間連続して出題されていた作図を元に考える問題は今年も出題されましたが、下書き用の図も添えられており、丁寧に考えればすぐに答えにたどり着く標準レベルの問題です。受験者平均得点率70.1%（84.1点／120点）、合格者平均得点率84.8％（101.8点／120点）と非常に高く、この学校を受ける受験生のレベルからしますと、高得点勝負の問題構成であったと言えます。

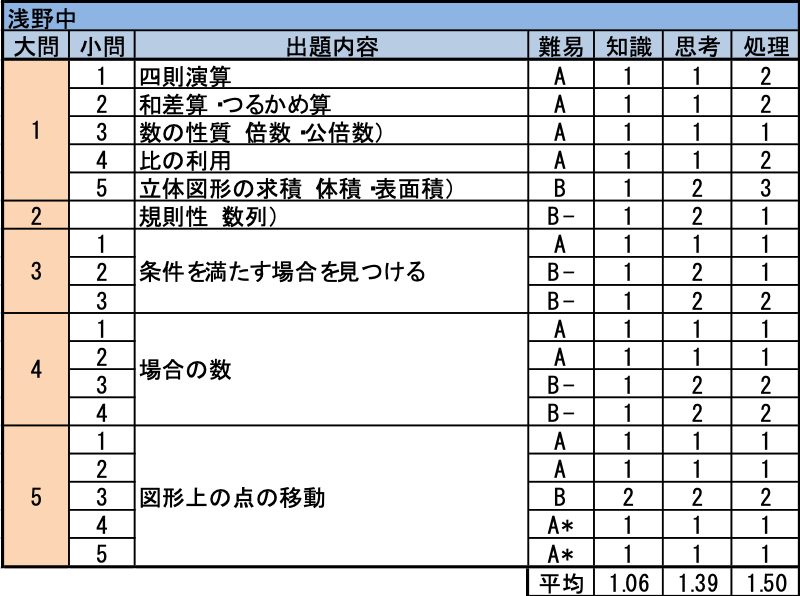
1. 特に難しい問題はありませんでした。（4）の遅れる時計と進む時計の問題も、時間と分の換算さえ間違えなければ確実に得点できる問題です。
2. 問題文が少々長めでしたが、その分誘導が多いため、問題文を正しく読み進めていくことができれば、答えを導き出すことができる問題です。
3. 一方の数が変わるとそれに伴いもう一方の数も変化する関係を元に調べさせる問題ですが、（1）は計算のみの基本問題です。（2）（3）は調べ上げの作業が少し必要ですが、調べ上げる範囲もある程度絞り込めるため、膨大な作業が必要という問題ではありません。
4. 塾のテキストでもよく見かけるじゃんけんについての場合の数です。標準レベルの問題と言えますので、確実に得点したいところです。
5. 下書き用の図を上手に利用できれば特に難しいという問題ではありません。（1）（2）は三角形の相似。（3）（4）は補助線入りの下書き用の図を活用できれば、特に難しくはありません。（5）も正六角形が同じ大きさの正三角形６つの集まりであるという多角形の性質の基本知識が定着できていれば、確実に解ける問題です。

　今年の出題傾向は「○○算」といったいわゆる中学受験算数の特殊算のテクニックをフル活用しなければならない問題は見当たらず、むしろ数の性質や図形の性質、長めの問題文も読み飛ばさずにしっかり読み込む読解力など、基礎力を問われる出題が中心であったと思われます。塾のカリキュラムで言えば、４年生・５年生のテキストの標準問題レベルがしっかり習得できていれば、確実に対応できた問題群と言えます。
　最難関校との併願を考える場合においても、４年生・５年生までは、基礎力の徹底した習得を心がけて下さい。まず、基礎計算力は必須となります。「正確で早い」計算力を４年生・５年生の２年間では特に徹底することを心がけて下さい。文章題につきましては、手を動かしながら考える訓練をして下さい。問題文を読んで、その条件を整理するための線分図や面積図、また平面図形や立体図形では、どこに補助線を引けば解法が見つかるのかなど、実際に自分の手を動かしながら考える試行錯誤力がとても大切です。しかし、一朝一夕に出来るようになるものではありません。時間をかけて丁寧に書く必要はありませんので、フリーハンドで素早く線分図や図を書き、頭の中を整理しながら考える試行錯誤力は、６年生になってからの学習に非常に役立ちます。
　その上で、６年生は、４年生・５年生で積み上げた基礎力に更に磨きをかける「実力練成」期間となります。少なくとも塾のテキストの標準レベルの問題まではしっかりと対応できる力をつけることを目標にして下さい。浅野中学校につきましては、今後再び難易度が上がる可能性は十分に考えられます。その際に、やや難易度の高い問題までしっかり対応出来るかどうかが、合格を左右します。そのような問題では、問題文を読んですぐに解法が分かる単純な問題はなかなかありません。その際に効果を発揮するのが、手を動かしながら考える試行錯誤力となります。
また、過去問に取り組む際は、過去３年間ぐらいまでは当然ですが、少し昔の過去問にも取り組んでみるなど、様々な難易度の問題に触れ、初見の問題に対する対応力を着けてゆくことを心がけて下さい。