2018入試分析算数

目次

開成中
麻布中
武蔵中
桜䕃中
女子学院
雙葉中
筑波大付属駒場中
駒場東邦中
豊島岡中
渋谷教育学園渋谷中
早稲田中
早稲田実業中
慶応中等部
聖光学院
栄光学園
渋谷教育学園幕張中
芝中
フェリス女学院

総評　算数

　教育改革、そして2020年から始まる大学入試改革が間近に迫っており、昨年末にはセンター試験に変わる新テストの試行テスト問題が公表されるなどその具体像が見えつつある。それに伴い中学受験全体で見ると英語の導入やAO型入試などの新たな形が導入されるといった変化が出てきている。

　ところが今年の算数の入試問題についてみると、今回分析の対象とした範囲では全体として入試改革を意識した変化は見られなかった。今回の教育改革では「知識・技能」「思考力・判断力・表現力」「主体性・多様性・協働性」を学力の3要素として掲げているが、算数という科目の特性上、特に難関校では前2つは従来から問われ続けていること、および最後の主体性等は筆記試験での測定が難しいこともあるのだろう。

　一方で、難関校では個々の学校ごとの出題傾向は従来通り顕著であり、強靭かつ緻密な処理が重視される桜蔭、必要とされる知識は最小限だがその場での作業を通じて考える力が求められる麻布といったように学校ごとのポリシーが表れているようである。開成の急激な易化、傾向変化は話題の１つだが、以前から年によって出題傾向や難易度が大きく変わることがよくあるという点では傾向通りとも言え、あえて傾向を固定しないことで何を出されても対応できるだけの力を求めていると見ることもできる。

　このような学校ごとの出題に対応するためには過去問や塾での志望校別講座を通じて傾向に合わせた対策が必要になる。このような授業は6年生になってから、特に後半に重点的に行われることもあり、5年生や6年前半までは定型的な解法を習得する時期、その後は過去問に合わせた学習を重点的に行う時期という認識が一般的である。しかし大筋では正しいとしても、時期ごとに学習内容を完全に分けて考えてしまうことには問題がある。例えば桜蔭が求めているような強靭な処理力は6年生後半になって身につけるものではなく、もっとそれ以前からの練習の積み上げがものを言う。また麻布で求められる作業力、思考力についても6年前半までずっと解法習得のための暗記一辺倒で学習していた子がある時期から急に切り替えられるわけではなく、解法習得が中心の時期であってもきちんと手を動かして考えるという学習を継続して行っていることがその土台となっている。従って問題にクセのある難関校の受験を考えている場合には、6年生の以前から志望校を見据えた上での学習の土台作りが大切である。

　ところで、今年の入試の１つの特徴として以前より問題が易しくなった学校が多かったことが挙げられる。例年分析のために問題を解いていると確かに力作だとは感じつつも受験生が時間内に解くのは酷だと思われる問題がいくつも見られたが、今年はそのような問題は皆無に近かった。少々寂しい気はするものの、いくら腕によりをかけて作った問題でも合否にほとんど影響を与えないばかりか、過去問にあっても「捨て問」として見向きもされないことが多い現状ではやむを得ないという側面もある。そればかりかほとんどの受験生が解けない問題がなくなったことで以前よりも合格者平均と受験者平均の得点差、すなわち算数が合否に与える影響がより大きくなったという学校も多く見られる。

　この「易しさ」には2つの側面がある。1つ目は難しめのパターンではなくより標準的なパターンが問われており、特に今年は立体切断で以前ほどの複雑な問題ではなく定型的な形のものが多く目についた。難しい問題を学習していたのだからもっと素直な問題であればみんな解けることが普通かと思いきや、実際にはそうはなっていない。これは多くの塾のカリキュラムが最難関校対策から逆算して作られているため、多くの子には早い時期からオーバーワークを強いることになっている、そのため十分な理解を伴わない消化不良状態のまま問題を解くことになっていることも影響しているように思われる。定型的であっても単に難しい問題を繰り返して解けるようにするのではなく、納得を伴う土台作りに基づいた理解および問題解決の重要性を再認識すべきであろう。

　もう１つの側面は、麻布や栄光に代表される以前から塾のカリキュラムと一線を画した出題を続ける学校において、きちんと作業して素直に考えれば十分に手が届く問題が増えていることである。１つ目に挙げたパターン問題については難関校受験生であればクリアできていることが多く、今年のパターン問題だらけの開成での平均点の高さはその証左でもある。しかし昨年、一昨年と続いたパターンから外れたその場での読解を求める問題では得点率が大きく下がり、難関校受験生であっても形が変わった問題にきちんと対応できる子はそれほど多くない。そこで出題のスタンスは変えないまま、きちんと考えられる子であれば十分手の届くラインに問題を設定する、あるいは考えるためのヒントが増えるなどの変化がみられるようになっている。実際に栄光では10年前に比べると圧倒的に小問数が増加しており、また駒東や渋渋、早実などでは以前よく見られた難しい問題が大きく減少している。しかしこの「易しさ」はきちんと手を動かして考えられる子にとってのものであり、パターン暗記中心の学習だった子には以前と同じようにしか感じられないものである。

　このように問題が易しくなったといっても、普段の学習においてきちんと納得した上で問題を解けるようにするといった「知識・技能」、および見たことがない問題でも手を動かして条件整理や具体的に書き出すといった「思考力」を養うといった地に足の付いた学習が大切であることには変わりなく、むしろその成果がより大きく反映するようになったのである。またその過程においては一方的に教わり続けるという受け身の姿勢ではなく、何としても自分で考えて問題を解く、理解しようとする「主体性」が必要である。このことは冒頭に述べた教育改革の方向性とも大きくずれてはおらず、真っ当な学習をしていれば目の前にある一見大きそうな変化にも慌てる必要はないであろう。

開成中

　近年は目新しい難しめの問題が続いていたため、十分に対策をして臨んだ受験生が多かったのではないだろうか。しかし今年はそんな受験生に肩透かしを食らわせるような典型問題のオンパレードで、合格者平均点73.9点（85点満点）と非常に高くなった。算数のできない受験生は間違いなく弾かれたであろうが、算数で逃げ切ろうと考えていた場合は目算が狂ってしまったであろう。

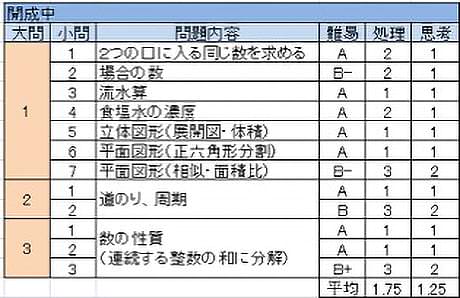
1. まるで塾のテストの前半のような、定型的手法の確認問題。
2. 周期性の問題に曲線の長さが加わっており、3.14をうまく処理しないと計算が煩雑になるが、それだけである。
3. 数表のように見えるが、実質は整数を連続する整数の和に分解する問題であり、類題経験のある人も多いであろう。(3)も典型問題の一種だがやや発展的であるため、すべて調べ切れれば多少は優位に立てたであろうか。

　出題者の気まぐれかと思ってしまうくらいに年によって大きく出題傾向が変わることがあるのも開成の特徴である。過去にも今年のような典型問題多数で構成されたことがあったが、このような年には得点率は大きく跳ね上がる。従って塾で学習するタイプの問題は発展的なものも含めて確実に押さえておくことは最低条件である。またこのようなことが起こる可能性も考慮して、算数以外の科目の穴を算数でカバーすることを当てにし過ぎない方がよい。
　とはいえ、今年のような問題が続くとは思わない方がよい。出題傾向が安定しない以上、どのようなタイプの問題が来ても対応できるように準備しておく必要がある。昨年、一昨年と続いた目新しい設定の状況把握が大変な問題では得点率が大きく下がり、このような問題ができるようになると出された場合に大きくリードできる可能性がある。また方針は単純だが計算が煩雑な問題が並ぶ場合もあるため、計算力も十分につけておく必要がある。目の前の傾向に振り回されずにオールラウンドな力をつけること、これが開成対策に最も大切なことである。

麻布中

　昨年に比べ見慣れたタイプの問題は減少した。しかし実際に手を動かして考えてみると状況把握がしやすいものが多く、パターン暗記中心の学習をしていると難しく感じられ、普段から手を動かして考えてきた子には取り組みやすく感じられたのではないだろうか。

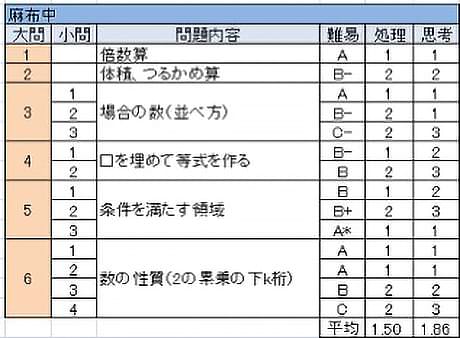
1. 倍数算の基本問題。
2. 回転体の体積だが、未知数を求めるところにつるかめ算の考えが使える。
3. 記号の並べ方。(2)までは作業で何とかなる。(3)はここまでの作業を元にどういう場合があり得るか考えて解くのだが、場合を見落とさないように注意。
4. 時々見られるパズルのような問題で、数の感覚を元にあたりをつけてやってみるしかない。時間を忘れてはまってしまわないように。
5. 時間内にクモの移動できる領域を考える。どの辺が最も近いかで場合分けして考えるとよい。(3)は(2)ができた子に対するおまけ問題。
6. 2の累乗の下k桁に関する問題。見慣れた設定で(3)までは作業力でも押し切れるが、(4)の下3桁はさすがに不可能。(2)の意味深な設問にどのような意味があるのか考えてみることが突破口となる。

　今年は少なかったが、例年3分の1程度は塾で学習するタイプの定番問題が出されるので、基本的な解法はきちんと身につけておくことも必要である。ただし発展的な手法を知っていることで有利になるような問題はまず出ないので、あらゆるパターンを網羅して覚えようとする必要はない。むしろわからない問題に対してすぐに解答をみて覚えるような学習習慣は麻布対策として百害あって一利なしである。
多くの問題は見たことがないような設定であるが、問題に従って順に作業しながら考えることで糸口がわかるように作られている。従ってこのようなタイプの問題に対してしっかりと手を動かしながら考えることが最良の対策であり、麻布の過去問はそのための最良のテキストでもある。

　5年生までに定型的な解法を一通り身につけ、6年生（後半）で過去問に合わせた練習を中心に行うのが一般的な塾のスタイルである。しかしこのような問題に対応する練習はある時期から特化して行うものではなく、普段から熱中して、面白がって考えるという経験がものを言うのである。麻布中を志望校に考えている場合には、塾で解法を身につけるような学習が中心になる4、5年生の時期であっても、そのための勉強、目の前の1点に囚われすぎず、応用問題に対して「ああでもない、こうでもない」と楽しみながら考える余裕を持った学習をしていくことがよい。

武蔵中

　大問４問構成に変わりはないが、今年は図形に関する問題が少なかった。例年目新しい問題が出される４がどこかで見たような題材で取り組みやすいが、他の問題で平易なものが少なく、全体で見れば例年並みの難易度であった。

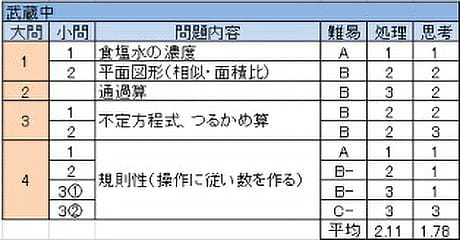
1. 小問２題。(1)は濃度の平易な問題。(2)は今年唯一の図形だが、解答を得るために考えることが多く、小問としてはやや難しめである。
2. 見た目に目新しく見えるが、状況を整理して通過算に注目できるとほぼ一直線に解決する。1問の中で聞かれていることが多い（その上解答欄がない）ので、すべてに答えたか細心の注意が必要。
3. (1)は売買損益に見えて整数条件から不定方程式に持ち込む、(2)は不定方程式に見えて実はつるかめ算になる。方針選択を誤らないことが大切。
4. どこかで見たような規則性の問題で、(3)①までは丁寧な作業で解決するが、(3)②は50個も調べられない。それまでの設問を解く過程で何に注目するのか読み取りながら考えることが必要である。

　細かい誘導が少なく、問題の下にある広い余白に考え方も含めて記述させるのが昔からの武蔵のスタイルである。例年前半３題は文章題、平面図形のどこかで学習したような考え方を使うことが解決できる問題が出されるが、誘導が少ない分解答に至る流れを自分で構築し、表現する必要がある。従ってこのような定型的な手法を学習する際においてもどういうときにこの解法が使えるのかといった点まで踏み込んで理解し、誘導がある問題であってももしそれがない場合にどのようにアプローチするかということも考えておきたい。また考え方を書くことは時間がかかる面倒な作業にも見えるが、このように1問に複数ステップを踏んで考える際には自らの思考を整理するというメリットもあるので、普段から意識的に行うようにしたい。
　とはいえ10年以上前と比べれば、目新しい問題については具体的な場合を調べさせる、理由を説明させる問題で着眼点を示すなど、考えるべき方向性を問題の中でヒントとして示している問題も出てきている。このような設問に対して単に１つの小問が解けて終わりとするのではなく、あえてその設問を設けた意図をくみ取りながら考えるようにしていきたい。

桜蔭中

　丁寧な読解に基づいた緻密な作業力と強靭な計算力に加え、近年は場合の数や調べ上げといった出題も増えており、今年もその傾向は踏襲されている。今年は大問数が5題から4題に減少し、合わせて設問数の減少、途中過程を記述させる問題も減るなど一見して処理の負担は軽くなったようにも見える。しかし以前のような煩雑な処理を必要とする問題が復活しており、トータルで見ると昨年同様の負担感、難度であった。

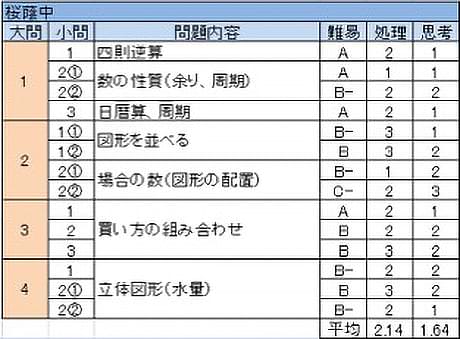
1. (1)計算が2問から1問に減少した。(2)②15で割った余りでも繰り返すだろうという予想は立つだろうが、問題の意味を取り違えないように注意。 (3)過去問では祝日が影響したものもあったが、今回は結果的に考慮する必要はなかった。
2. (1)方針はわかりやすいが計算が煩雑になる、桜蔭にありがちな問題。(2)昨年から登場した場合の数。特に②はどのような場合に回転して同じになるかよく考える必要がある。
3. 3通りの買い方を組み合わせる問題。特別な考えは一切必要なく、丁寧に調べつくせるかが試されている。この位置に最終結果のみを求める大問が来ることは珍しい。
4. 水量の問題。方針に紛れはないが、計算が煩雑なうえ最終結果が不安になる数値である。実は最後の設問がそれ以前と無関係で最も考えやすく、途中の嫌らしい数値であきらめない精神的なタフさが必要。

　1問1問の考え方に難しいものはないが、緻密な作業、正確な処理といった点でのハードルは高く、見た目以上に得点しにくいのが桜蔭中の特徴である。このような問題に対しては見て学ぶ（方法を覚える）という学習は通用しない。必ず最後まで自分の手で解き切ることを欠かさず行うようにしたい。
　またこの計算力、処理力は6年生で本格的に志望校対策をしてから身につけるものではなく、小さいころからの訓練によって身につき、また計算に対するセンスが磨かれるのである。塾に通ってからが受験対策というのではなく、それ以前から多少煩雑であっても最後まで正確にやり切るだけの計算力はつけるようにしておきたい。

女子学院

　標準問題中心でてきぱきとした処理が試される構成は例年通りである。一昨年まで難化傾向あったものの、昨年易しくなり、今年も昨年同様に穏やかな問題が中心であった。とはいえパターン問題に若干の変化が加わっているので、冷静にそれらを見抜いて対処することが求められている。

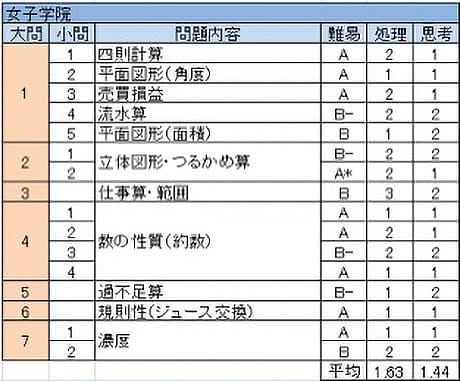
1. 小問集合。ほぼ難易度順に並んでおり、親切である。(4)では流水算＋旅人算では流れが無視できること、(5)は補助線1本で平行四辺形を作ることが気づきにくいかもしれない。
2. (1)でつるかめ算の利用がわかると一本道である。
3. 仕事算の定番に見えるが、範囲で処理することが求められている。
4. 見かけ仰々しいが、実質は約数と素因数分解の基本が問われているだけである。
5. どのバスにも先生が2人＝生徒の定員を2人減らすと考えれば過不足算の基本問題。
6. ジュース交換の定番そのものである。
7. 濃度に関する問題。落ち着いて状況を整理できれば難しくない。

　1問1問落ち着いて考えれば難しくはないものの、短時間で多くの問題を処理することが求められるところに本校の難しさがある。また以前は3枚目に難しい問題が配置されることが多かったが、近年は必ずしもそうではなくなっており、前から順に解いて時間が来たら終了だと取り返しのつかないことになる可能性がある。
　所々に混じるちょっと考えさせる問題についてはパターン問題そのものではなくても、その考え方のポイントを十分理解しておけば対策可能なので、自分の中に十分落とし込むところまで理解しておきたい。また時間がかかりそう、難しそうだと判断した問題については一旦後回しにして短時間で１つでも多く正解するための取捨選択も大切である。

雙葉中

　全体として見れば標準的な問題の考え方を組み合わせて解ける例年通りの構成であるものの、最初が計算問題ではなくなり、２から1枚目としては難しめの問題が配置されるなど、例年に比べ取り組みにくく感じやすいセットであった。

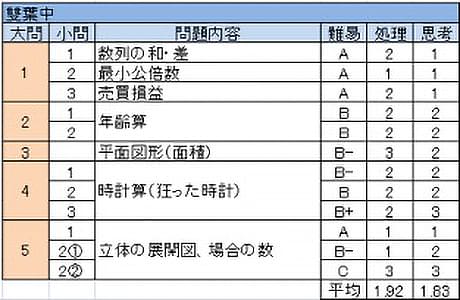
1. 小問集合。(1)が計算問題でなくなった点は例年と異なるが、取り組みやすい。
2. 年齢算だが、通常通り倍数算の考え方に持ち込もうとするとはまりやすい。妹の年齢が3通りしかないことからすべての場合を調べるとよい。
3. 図形の面積。例年通り1問を解くために複数の知識を要する。
4. 時計算だが、長針が逆回転しているため、角速度での旅人算という考えに立ち返って考察する必要がある。
5. 立体図形。(2)②ですべての場合を調べつくすのは難しめである。

　昨年、今年と難化傾向にあるが、どこかで見たような問題そのものの出題が減り、それを組み合わせて考える問題が増加している。「こういう状況が与えられたときにはこの考え方が使える」というところまで落とし込んだ理解をしておくこと、および誘導がない場合にそれを組み合わせて流れを構築することが求められている。
　後者について、本校ではほぼすべての問題で途中過程を書くことが求められるが、これは自らの思考を整理しながら考える点で有効である。塾のテストなど短時間で多くの問題を処理する際にはすべてを書くことはできないが、じっくり時間をとって1問1問式などをわかりやすく書きながら学習する時間も並行してとるようにしたい。

筑駒中

　例年順を追って追跡する、規則が見つかるまで調べるといったその場での作業力が重視されているが、近年は３のような平面図形に関する問題も混じることが増えている。今年は１と３が難しめ、２と４が易しめであったので、40分という短い時間内で高得点をとるには問題に取り組む順序も大切であった。

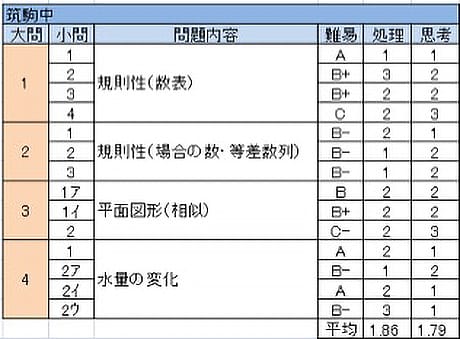
1. このタイプは周期があることは経験的にわかるであろう。しかし20列が周期であるため、まともに計算すると(4)は大変である。(3)の0の位置を活かして絞り込めるとよいが、ごり押しで時間をかけすぎた結果、後の問題で時間不足にならないよう注意。
2. (1)を正しく調べて等差数列であることがわかれば簡単である。
3. (1)すでにたくさん線が引かれているが、さらに線を加えて相似を作る必要がある。(2)は(1)に倣って補助線を引いてみるとよい。全滅も全問正解もあり得るという点で大きく明暗を分ける１題といえる。
4. 問題に書かれている通りに順を追って作業していくと解決する。ただし最後の問題なので時間をきちんと残せたか。

　近年は発想面で難しい問題はないが、時間が40分しかないのが厳しいところである。まずは時間をかけてでも正解できることが前提だが、その上でその作業をいかに短時間で行うかが重要である。計算力などの作業の速さだけでなく、どこに注目して考えると速く調べられるかといった着眼点の振り返りも大切にしたい。
　受験者のレベルを考えると思わぬ合格はあり得ないが、思わぬ不合格は十分にあり得る。特に時間が短いゆえのあせり、取捨選択のミスは大きな影響を与える。ある程度問題が解けるという目途がついた後は、時間内で１問でも多く正解できるよう、時間を測った実践的な練習をしっかり行うようにしておきたい。

駒場東邦中

　昨年急に易しくなったが、今年もかつてのような考え込ませる難問はなく、比較的取り組みやすい。とはいえ丁寧な作業を元に考察させる問題が所々に混じっているため、それらにどれだけ取り組めたかで十分に差はついたであろう。

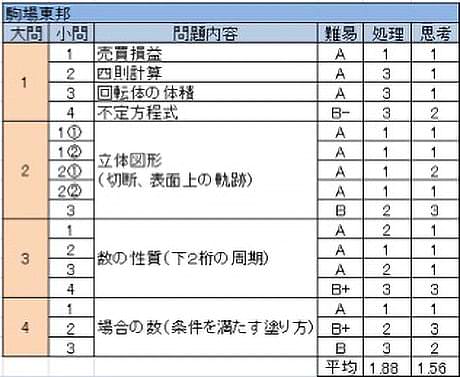
1. 小問集合。(2)に計算問題が来るのは珍しいが、実際(1)が易しく、(2)以降は考え方に難しさはないもののいずれも処理量が多い。
2. 立体図形に関する問題。(2)までは定番知識の確認で易しい。(3)は平面図形でよくみられるひもにつながれた運動を立体で考えさせている。
3. 累乗の十の位の周期を考えさせているが(3)までは平易。(4)は周期が4と5の最小公倍数20になることさえわかれば後は調べるのみ。ただしa=1の場合だけは別扱いになることに注意が必要。
4. 場合の数だが、(2)は計算による処理、(3)は丁寧な調べ上げと両側面で十分な力が必要である。

　発想面での難しさはなく、丁寧な作業とそれに基づく考察が求められている。大問の前半に調べさせる設問があるあたりに出題者の親心が感じられるが、これがなくてもまずは調べてみる、わかっていることを整理してみるといった作業を行うことは大切である。
　ここ2年は穏やかなセットが続いたが、これが来年も続くとは限らないので、以前のような問題が出されたときにどう対応するかということも想定して練習しておきたい。

豊島岡中

　易しい問題から、やや難しめの問題まで幅広く出題される。受験者レベルの高さを考えると易しい問題での取りこぼしは許されず、難しめの問題にもある程度食らいつく必要があるだろう。

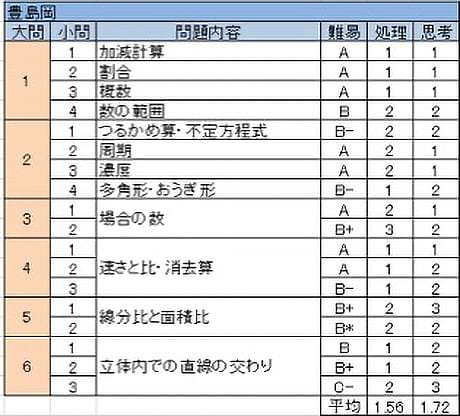
1. (4)□×□＝12となる数の範囲を考えるだけだが、中学受験では見慣れない問題。
2. (1)つるかめ算と不定方程式の2つの条件を組み合わせて考える。
3. カードの組み合わせを考えて並べるという場合の数の定番。(2)は少々複雑で間違えやすい。
4. (2)までは消去算、(3)は旅人算であることがわかれば難しくない。
5. (1)で2つの三角形の面積が等しいという条件をどう活かすかが最大のポイント。その後は定番の手法で解決できる。
6. 空間内での2直線の交わりを考える。適切な平面を取り出す必要があり、女子校の中では程度の高い問題。例年立体図形は難しめであることが多い。

　一部にやや難しめの問題も出されるが、そのほとんどは難関校向けの授業で扱われるような発展的な問題まできちんと押さえておくことで対応できる。例年得点率は高いので、難しめの問題であっても逃げずにきちんと考え方を理解、吸収するようにしておくこと必要となる。

渋渋中

　以前はかなり難しめの問題が並んでいたが、近年はその中に解きやすい問題も多く混じるようになってきている。今年はほとんどの人が手を付けられないだろう難問がなく、きちんと対策してきた人であれば高得点も狙えるセットになり、算数が合否に与える影響は大きくなったものと思われる。

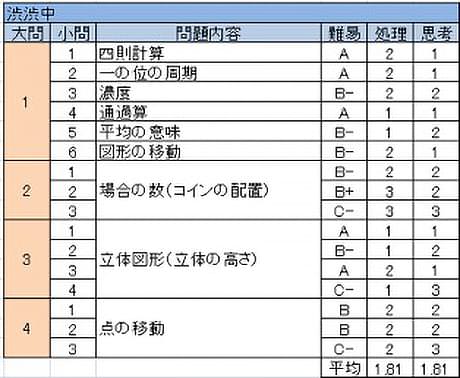
1. 昨年同様に小問は比較的取り組みやすいものばかりである。(5)の理由説明は渋渋では珍しく、大学入試改革を意識したか。
2. コインの配置に関する場合の数。基準を設定して丁寧に調べていくのだが、高い作業力が求められている。
3. 立体を切断し、切断面を下に置いたときの高さを考える問題で、(3)までは平易。(4)は平面図による立体の把握ができるとよい。
4. 点の移動に関する問題。典型問題にひねりが加わっているのでどういう場合かしっかりと把握することが必要。特に(3)はPQで「2つの四角形に分ける」とは言っていないことに注意。

　これまでは5～6割とれれば十分と言われていたこともあったが、今年はそれでは合格ラインに届かないであろう。手の付けやすい問題が増える傾向にあるので、問題をよく見極めてできるものはきちんととること、その際に難易度変化があることも想定してこれだけできれば十分と先に決めつけず、できるものは1問でも多く貪欲に狙う姿勢が大切である。

早稲田中

　大問５問で、どこかで見たような雰囲気のある問題が多く並ぶのは例年通り。また難問も易問も少ないことも例年と同じであり、ある水準を超えれば高得点も狙えるが、そうでないと撃沈しかねないセットである。

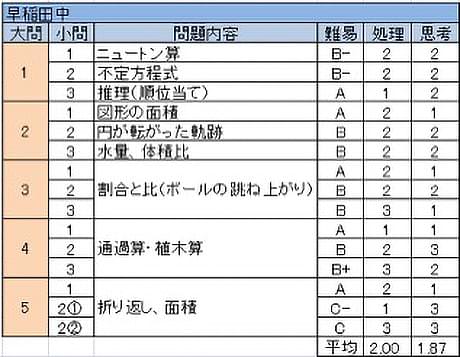
1. (1)1問目からぎょっとしそうだが、問題文の雰囲気からニュートン算と察したい。(3)の推理は早稲田中定番の１つである。
2. (1)は同じ形の図形が昨年の早実にあり。
3. ボールの跳ね上がりという有名テーマ。段差が多いので丁寧に処理したい。
4. 通過算に車両の数を考えるところまではありがちな問題だが、さらに連結部分の長さも考えるアレンジがなされている。考えるべきことが多く、混乱しないよう注意。
5. (1)正方形の周りを正方形で囲む。(2)①の作図でどこの点を通過するか正確に把握する必要がある。

　定番問題のやや難しめのものがよく狙われるが、近年はそれをさらに一ひねりした問題が多くなってきているので、難しめのパターンについても考え方をしっかりと理解して押さえておく必要がある。
　また問題の難易度が似通っているので、自分の解けそうな問題を見極めて１つ１つ確保していくといった問題の取捨選択も大切である。

早稲田実業中

　数年前までは早実の算数はとにかく難しい、というのが相場であった。ところが近年は標準レベルの問題も多く出されるようになり、今年もきちんと学習していればある程度の点数が見込める、学習の成果が反映されやすいセットであった。

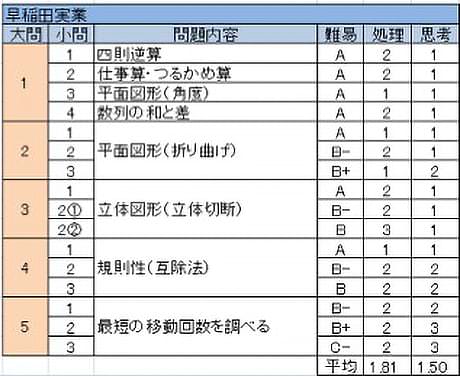
1. 平易な小問４題であり、全問正解が望まれる。
2. 紙の折り曲げに関する問題。(3)は時々見かける問題であるが、初見の場合は考えづらいかもしれない。
3. 複数回切断で難しそうに見えるが、１つ１つの切り方が交わらず、オーソドックスな切り方の組み合わせのみで解決できる。
4. 紙の切り分けに関する規則性の問題。類題多数だが、経験がなくてもその場での作業で容易に構造がわかるだろう。
5. 白玉を最短で移動する方法を考える。(1)(2)の作業で最短になる移動方法を見出すことが大切である。

　難しすぎる問題だと一部の算数が得意な子は圧倒的に優位に立つものの、合否ラインでの弁別性は低くなる。このくらいの難易度だと努力した分がそのまま点数として表れ、かつ算数が合否に与える影響も大きくなるという点で好ましいといえるだろう。
　とはいえ、再び以前のような難問ぞろいのセットが出てくる可能性も否定できない。その場合は平均点もかなり低くなる（2015年は3割未満）ので、落ち着いて解ける問題を解くという心構えはしっかりと持っておきたい。

慶応中等部

　前半に小問12問、後半に大問４題（小問数8）の全20問構成は例年通り。前半に基本的な問題が多く並んでいるのはいつも通りだが、今年はこれまで後半の一部に見られた難しめの問題がなくなったためさらに易しくなった。

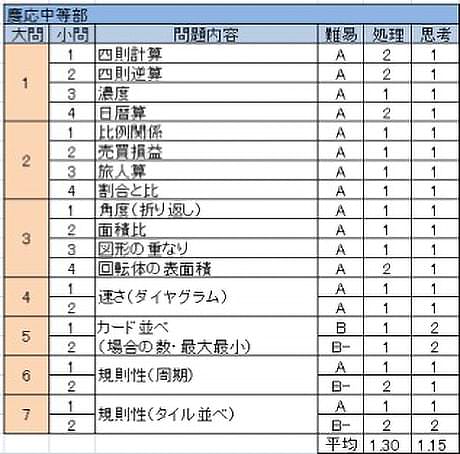
3. までは基本的な小問で、全問正解したい。
4. 親切にもダイヤグラムがかかれているので、相似を利用するとよい。
5. (1)の場合の数は今年の中では最も差がつくか。
6. 周期の定番だが、数字が大きいので○×でなく範囲できちんと処理する。
7. (2)ア、イに入り得る枚数を調べ、組み合わせを考えるとよい。例年ここには難しい問題があったが、今年は最後まで穏やかであった。

　受験者レベルを考えるとかなり易しく、１つの穴やミスが命取りとなる。普通の問題についてはいつ、何を出されても確実に正解できるようにしておく必要がある。
　また算数が得意であっても全くアドバンテージにはならないので、他の科目に穴がある場合には算数で挽回しようとは考えず、その科目の対策をきちんと行う方がよい。

聖光学院

　例年通り大問５題（内１題は小問集合）で、見ただけでは手の付けどころがわかりにくいが、状況が見えるとすっきりと解ける問題で構成されている。今年も昨年同様に難しい問題がなかったため、しっかりと対策をしていれば高得点も狙えたであろう。

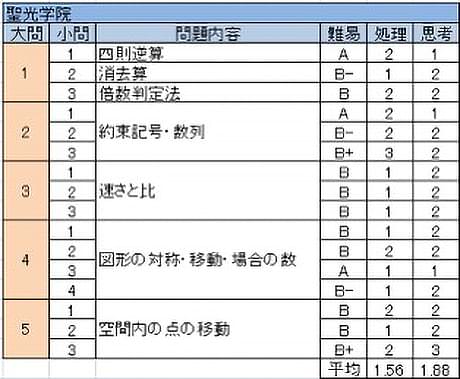
1. (2)5人の年齢の和だけが聞かれていることに注目できるとすぐにわかる。(3)条件の厳しいところから順に調べていく。
2. 約束記号。(2)1+2+･･･+63＝2016は2年前の受験生であれば常識だが…。(3)最初から順に調べることでおなじみの分数列の和になることがわかるとよい。ただし計算は大変。
3. 問題文は長い。しかしそれぞれの設問ごとのポイントが見えると簡単な計算で解決ができる。
4. 1つの図形を題材に対称、場合の数、平行移動と多くのことを聞いている。各設問が無関係に解けるので、前半の場合の数でつまづいてもあきらめないことが大切。
5. 仰々しい設定だが、3方向を独立したものとして考えるとよい。(2)(3)の点の通過領域は境界を考えると何ができるかわかるであろう。

　見た目に威圧感があるため、初めて過去問に取り組む際には手を付けにくく感じやすい。しかし状況が見えた瞬間にこれまで学習した手法に容易に帰着できるので、この状況把握が最大のポイントとなる。そのためには頭の中だけでなく、手を動かして図やグラフに整理する、具体的に調べてみるといった作業が特に重要である。

栄光学園

　塾で学習する問題とは一線を画し、目新しい問題や問いかけ方で思考力を問い続けるのが一貫したスタイルである。昨年はこのスタイルを維持しつつ個々の問題はかなり易しくなったが、今年は一転して以前のような難しさとなった。

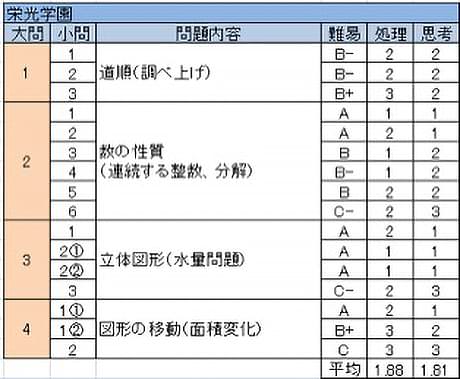
1. 道順の問題だが、右ページにマス目が与えられている通り、丁寧にすべてを調べつくすことのみがストレートに試されている。
2. 連続する10個の整数を用いて様々な角度で問われている。(3)の理由説明、(4)の最も極端な場合を考えるなどは栄光頻出。(6)連続10整数の和が25の倍数の場合だけ調べればよいことに気づくか。
3. 水量に関する問題で、(2)までは塾のテキストにそのままあるタイプの問題。(3)が本題で、どのような場合に条件を満たすかが考えどころ。
4. 図形の移動だが、2つの図形が重なる部分を丁寧に調べつくすことで解決できる。本問も作業力がすべてである。

　栄光の算数でよく問われるのは、すべての場合を調べつくすこと（今年では１、４）、条件を満たす場合を見出すこと（２と３の一部）であり、パターンの習得よりもその場での作業力に重きが置かれている。従って過去問を中心に自力ですべての場合を探し出す練習が大切である。その際には闇雲に調べるのではなく、どういう基準を設定し、どういう順序で考えるとうまく調べつくせるのかといった視点を特に大切にしたい。

渋幕中

　例年通りの大問5題構成であるが、近年難問の多かった場合の数が取り組みやすい問題となるなど手の付けやすい問題が増えた分、全体としてやや易しくなった。

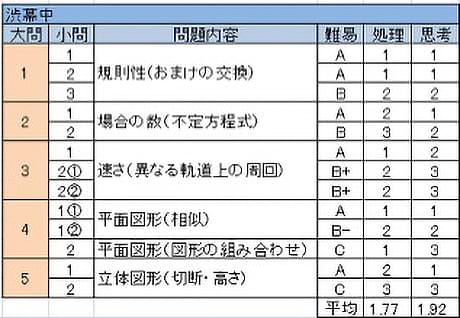
1. おなじみの設定の問題に2通りの交換方法がある点でひねりが加わっている。(3)は6枚集めた方が多く受けとれることに気づくとよいが、最後の詰めで誤らないよう注意。
2. ゲームの得点に関する問題で、不定方程式を満たす場合を丁寧に調べつくすのみである。場合の数は近年難しい問題が多かったが、今年は取り組みやすい。
3. 周回上の旅人算だが、3人の経路が異なるなど状況把握がしにくい。(2)で与えられた情報からBの動きを特定できると優位に立てる。
4. (1)が定番問題、(2)は補助線を引いて図形を見出す問題という構成は昨年と同じ。実は(2)で題材となっている三角形自体も昨年と同じであり、これに気づくことで問題の意図とは無関係に答えられた受験生もいたかもしれない。
5. 3年連続の立体切断である。(2)は体積経由で考えることになるが、四角錐の体積を考えると計算が大変になり、伸ばして大きいいつもの三角錐を見出すのは気づきにくいと、いずれにせよ時間内に解くのは大変な問題である。

　１問１問を解くために必要な手法は通常学習する範囲を超えるものではない。とはいえ文章題では状況を整理して把握する、図形問題では定型手法が使えるように図を復元するなど、算数で差をつけるにはパターンの習得以上にそれを用いて考えるという練習が大切である。解説を聞く、読むなどして納得してできるようにするだけでなく、見たことのない問題に対しても手を動かしながら試行錯誤する時間を多くとることがこのような問題への対応力につながるであろう。

芝中

　ほぼ小問に近い形式が最初から最後まで並ぶのが芝中の特徴である。１問１問は１行問題に近いが、多少ひねりが加わった問題が大部分を占めることが多く、例年得点率は高くなかったが、今年は素直な問題が増えたため得点しやすくなった。また例年必ず出されたグラフを用いた問題が登場しなかったことも今年の特徴である。

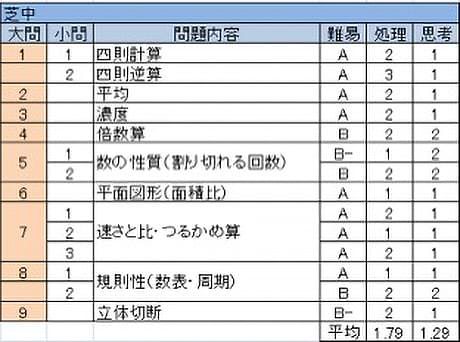
1. 例年通り煩雑な計算問題。このレベルを確実に合わせられるよう仕上げることが必要である。
2. 何の変哲もない平均にかんする問題だが、仮平均を使うと処理量が減らせる。
3. 濃度の平易な問題。
4. 倍数算だが、差一定と比の処理（分配法則）という2つの要素が絡んでいる。今年の中ではやや難しめだが、例年はこの難易度の問題が多く並んでいる。
5. 割り切れる回数の定番で途中だけ抜き出している、素数でないという点で間違えやすいが、書き並べて調べ切ることも可能な量にしている分親切である。
6. 面積比は定番だが、例年に比べ圧倒的に易しい。
7. 速さの問題で(3)まであるが、最初から最後まで平易な問題が並んでいる。
8. 数表のよくある問題。(2)も難しくはないが差がつきやすいところ。
9. 立体切断の典型題。

　全体として平易になったが、昨年までに比べ合格者平均と受験者平均との差が大きくなり、実力差がよりはっきりと出る形になった。多くの受験生にとって「捨て問」と判断される問題がなく、易しい問題の中にもきちんとした実力がないと間違えやすい問題が配置されたためであろう。
　今年の難易度であれば塾で普通に学習する問題がきちんと押さえられていえば得点は難しくない。しかし昨年までは2つ以上の要素が組み合わさった、一ひねりした問題が多く並んでいたのでそのような問題が出されることも想定した対策が必要である。最初は解法を引き出そうとしてもうまくいかず、なかなか得点ができないが、考え方のコツ、すなわち問題の条件をきちんとつかんだ上で使えそうな道具を引き出す感覚がつかめた瞬間に一気に得点が伸びてくる絶妙なレベルに設定されているので、昨年以前の問題でも自信をもって臨めるところまで練習しておきたい。

フェリス女学院

　解答用紙はなく、問題の下の余白に途中の考え方も書かせる形式で、例年図形問題で近似値や中学範囲の知識を持っていると有利になる問題が出されやすい傾向がある。問題ごとの難易差が大きいことも例年通りで、今年は特に最後が最も易しいため、きちんと時間を残すことが大切であった。

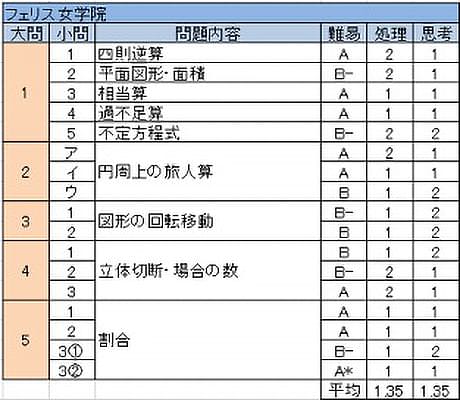
1. (2)5：12：13の直角三角形を知っていると一瞬だが、知らなくても面積を考えれば解ける。(5)桁数の分解に不定方程式を組み合わせている。
2. 円周上の旅人算は角速度で考えるという基本に従う。ウは合わせて何度動くかに注目できるとよい。
3. 図形の回転移動だが、軌跡から回転角を求めさせるという問い方は珍しい。
4. 立体切断で、(1)(2)(3)と設問が後に進むほど定番問題になっていく。
5. 学校のテストに出そうな割合の基本。強いて言うなら1.728＝1.2×1.2×1.2に気づくことだけがポイントか。

　図形など一部にクセのある問題が出されるためそれに特化して練習することがあたかもフェリス対策のように思われやすいが、塾で学習する普通の問題を普通にきちんと解ければ十分高得点をとることが可能である。クセのある問題については過去問を解く段階で慣れればよいだけなので、いわゆる「傾向と対策」に振り回されず、普段からのオーソドックスな問題の学習をしっかりと行うようにしたい。